3.4 4D Basics and Skills

Overview
| TCCNS Course | MATH 1332: Contemporary Mathematics |
| UT Austin Course | M 302: Introduction to Mathematics |
Introduction
Suggested Resources and Preparation
Materials and Technology
For the instructor: Copious images and manipulatives will be effective for this lesson. You'll want to explain that these are technically 3D objects, and that 2D objects are abstract and we must imagine them. Manipulatives can include:
basketballs, tennis balls, or other hollow balls for spheres;
lacrosse balls or billiards balls for balls;
children's ring stacker toys or hula hoops for toruses;
diving rings, donuts, or welded rings for solid toruses;
metal or plastic washers for annuluses;
paper cutouts for annuluses, disks, or polygons;
chenille stems or pipe cleaners, which can be formed into many 1D shapes.
Prerequisite Assumptions
- It is assumed that students have learned that "the area of a circle is \(\pi r^2\)" and similar formulas. Unfortunately, in topology there is a significant difference between a disk and a circle, and so the vocabulary should be treated explicitly.
Overview and Student Objectives
Lesson Length
50 minutes
Lesson Objectives
Students will understand that:
- 3D objects are defined as objects that have volume.
- 2D objects are defined as objects that have area but not volume.
- 1D objects are defined as objects that have length but not area.
- 0D objects are defined as objects that have no length, area, or volume.
- The boundary of an object always has one fewer dimension than the object has.
Students will be able to:
- Identify the number of dimensions in mathematical objects (such as line segments, circles, disks, annuluses, toruses, solid toruses, spheres, balls, polygons, and polyhedra).
- Identify the boundary of mathematical objects (as listed above), if it exists.
4D Basics and Skills
Dimension and Boundary
Terms
- Technically, the number of dimensions an object has is the smallest number of coordinates you need to describe any point in it. But these working definitions are better for this class and more intuitive:
- If it has no length, area, or volume, then it is 0-dimensional.
- If it has length, but not area, then it is 1-dimensional.
- If it has area, but not volume, then it is 2-dimensional.
- If it has volume, then it is 3-dimensional.
- The boundary of an object are all the points in the object that are adjacent to parts of the object and points that are not in the object. You can approach these points of the object both from outside and inside the object. (This definition is somewhat tricky, and it is best learned with lots of examples. Definitely watch the video below.)
We've all learned that "the area of a circle is \(\pi r^2\)." But there's a difference between a circle that is empty inside, or just a ring, and a circle that is shaded inside, or a disk. An infinitely thin hula-hoop is 1-D, and it has no area. Circles surround area, they contain area, but they do not have area. This video has more examples like this one.
https://utexas.hosted.panopto.com/Panopto/Pages/Viewer.aspx?id=5874418d-58f3-428c-867f-ac080038a326
Understanding what a boundary looks like in various dimensions will be very important for the next few lessons.
https://utexas.hosted.panopto.com/Panopto/Pages/Viewer.aspx?id=72ee929f-dc32-4a23-bcfd-ac080038caed
Boundary Examples
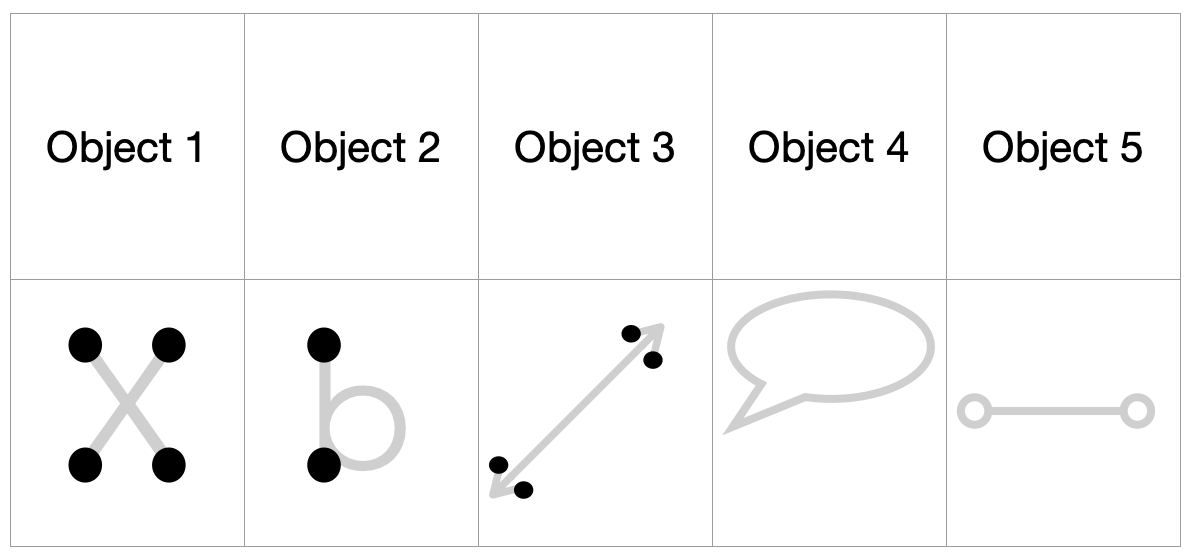
If we imagine a sans-serif Latin alphabet as infinitely thin 1-dimensional objects, then the boundaries of those objects have to be 0-D. The boundary points will be the "stabby bits" or the "dead ends," points where you can only go one direction and stay on the object. The middle point of the letter X doesn't count, nor do the elbows on the letters E or D, nor do the T junctions on letters like T or B. You can see the boundaries of every letter here:
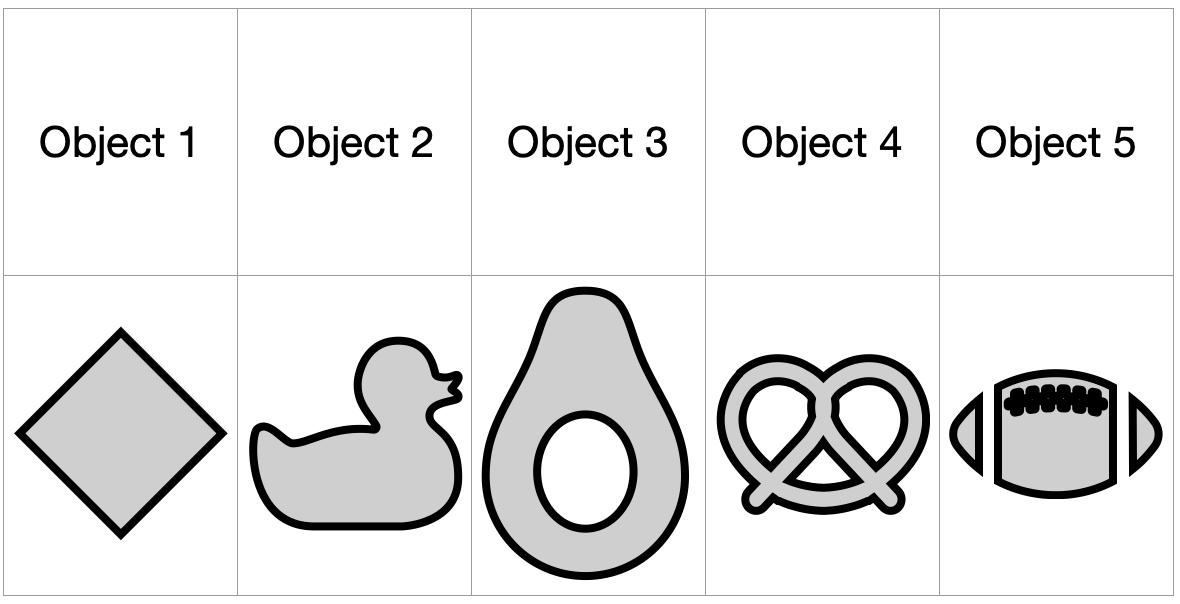
Boundaries of 2-D objects have to be 1-D and they represent sharp edges that you could get a papercut on. For example, the sphere, or empty soap bubble, has no boundary at all. The disk, or filled-in circle, has a boundary all around its outside edge. The annulus, or washer shape, has two circles for its boundary. You should not imagine these made out of paper and treat the surfaces that you can touch as the boundary. It's very important that we think of these objects as being 2-D strictly. It's like if you were holding the sphere in your hands, the space that your hands are occupying literally doesn't exist for the sphere. There are only two directions.

The Art of Analogy
One strategy for understanding these concepts is to use analogies to make statements about 4-D that were true. Mathematicians tried to set up the concepts of dimension to be super consistent, so that something that is true in one dimension is true in all of them in a way. For example:
The boundary of a 1-D object will always be 0-D.
The boundary of a 2-D object will always be 1-D.
The boundary of a 3-D object will always be 2-D.
The boundary of a 4-D object will always be 3-D.
I will use analogies throughout the videos to try to explain different facts about 4-D. Also, if you have questions about 4-D, you might try to create a similar question about 2-D or 3-D to help you build connections.
The Fourth Dimension as Time
Dimension is abstract; we get to apply it how we want. Think of it this way: the math problem "Solve 2x=10" has no meaning in the real world. But we can use it for different things. Splitting a $10 check between two people. Splitting ten pieces of candy between two children. Finding the midpoint on a ten foot board.
One of the easiest applications of the fourth dimension is time. I try to describe what it means to think of ourselves as four-dimensional beings if the fourth dimension is time. But remember that's not the only way to think of the fourth dimension.
https://utexas.hosted.panopto.com/Panopto/Pages/Viewer.aspx?id=b895c29c-7889-4670-97b0-ac58004860c2
For someone else's perspective, I like this illustrated clip describing people as four-dimensional beings.
Quiz Questions
| Question | Answer |
| 1 | 3 |
| 2 | 1 |
| 3 | 2 |
| 4 | 3 |
| 5 | 4 |
| 6 | 2 |
Question 1
What is the area of an infinitely thin circle of radius \(r\)?
- Area = \(2\pi r\)
- Area = \(4\pi r^2\)
- It has no area.
- Area = \(\pi r^2\)
Question 2
What is the boundary of an infinitely thin hollow triangle?
- It has no boundary.
- The three sides of the triangle.
- The inside and outside edges of the triangle.
- The three points.
Question 3
If a 3D object has a boundary, how many dimensions must that boundary have?
- One
- Two
- Three
- Four
Question 4
If a 4D object has a boundary, how many dimensions must that boundary have?
- One
- Two
- Three
- Four
Question 5
If a 5D object has a boundary, how many dimensions must that boundary have?
- One
- Two
- Three
- Four
Question 6
How many dimensions does an infinitely thin soap bubble have?
- One
- Two
- Three
- Four
Homework Questions
Question 3.4.1
Points in boundary:
1. four 2. two 3. four 4. zero 5. zero
Question 3.4.2
Number of pieces:
1. one 2. one 3. two 4. four 5. four
Question 3.4.3
Describe the boundary of these actual 3D objects and give the number of distinct pieces that comprise that boundary.
- tennis ball: one sphere on the outside and one sphere on the inside. Two pieces
- half of a tennis ball: the inner and outer half-spheres are now connected by the annulus created when we sliced. One piece.
- coffee mug: is usually a smooth solid ceramic object with no cavities. One piece, which is the outside surface.
- one foot length of pvc pipe: even though we think of pipe as having an inside and an outside, an ant could crawl over the edge into the pipe with no problem. The boundary is one piece (technically a torus).
- a large brick of swiss cheese: The outside surface we can touch is one piece. Then depending on how hole-y the cheese is, each distinct cavity contributes another piece to the boundary.
Question 3.4.4
One way we know we are in 4D space is if we need four coordinates to describe a point. Let's back all the way up to 1D world - a number line. Plot these points on the number line: 5, 2, -2.5.
- Is one number always enough to locate a point on the number line? Yes.
- Do you ever need two coordinates? No.
Question 3.4.5
Now draw x and y axes and plot these points: (2,3), (1,-2), (-3,0). This plane is 2D space.
- Can you locate any point on the plane with two coordinates? Yes.
- Do you ever need three coordinates? No.
- What would you say if I told you "Plot the point x=3?" I would say there are infinitely many points with x coordinate 3, so we need to be more specific.
Question 3.4.6
Mindset question. Responses vary.
Question 3.4.1
Imagine these objects as 1-dimensional. Describe their boundary and give the number of points that comprise that boundary.
Question 3.4.2
Imagine these objects as 2-dimensional. Describe their boundary and give the number of distinct pieces that comprise that boundary.
Question 3.4.3
Describe the boundary of these actual 3D objects and give the number of distinct pieces that comprise that boundary.
- tennis ball
- half of a tennis ball
- coffee mug
- one foot length of pvc pipe
- a large brick of swiss cheese
Question 3.4.4
One way we know we are in 4D space is if we need four coordinates to describe a point. Let's back all the way up to 1D world - a number line. Plot these points on the number line: 5, 2, -2.5.
- Is one number always enough to locate a point on the number line?
- Do you ever need two coordinates?
Question 3.4.5
Now draw x and y axes and plot these points: (2,3), (1,-2), (-3,0). This plane is 2D space.
- Can you locate any point on the plane with two coordinates?
- Do you ever need three coordinates?
- What would you say if I told you "Plot the point x=3?"
Question 3.4.6
Read this article on positive and negative self-talk and respond to the following questions:
- What are the things you say to yourself when you encounter something challenging at school?
- How does this self-talk make you feel? Do you wish it were different?