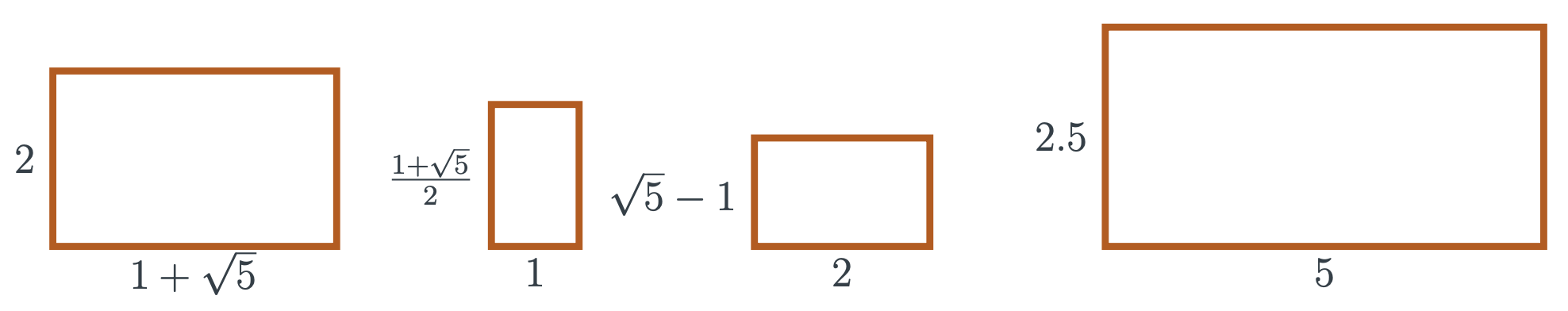3.2 Golden rectangles

Overview
| TCCNS Course | MATH 1332: Contemporary Mathematics |
| UT Austin Course | M 302: Introduction to Mathematics |
Introduction
Suggested Resources and Preparation
Materials and Technology
For the student: Grid paper, ruler
Prerequisite Assumptions
- It is best if students are able to rationalize denominators in fractions containing radicals, for example \(\frac{2}{\sqrt{5}-1}\).
- Students should be able to use the Pythagorean Theorem to solve for the hypotenuse of a right triangle given its two shorter sides.
Overview and Student Objectives
Lesson Length
50 minutes
Lesson Objectives
Students will understand that:
- Any rectangle where the ratio of long side over short side is the Golden Ratio will be called a Golden Rectangle.
- A Golden Rectangle may be subdivided into a square and a smaller Golden Rectangle. Moreover, this can be done infinitely many times.
Students will be able to:
- Test rectangles to see if they are Golden, given their measurements.
- Construct a Golden Rectangle on grid paper using a ruler.
- Construct an approximate Golden Spiral inside of a Golden rectangle which is subdivided into infinitely many squares. (Generally, students are instructed to use quarter circles in place of an actual logarithmic spiral).
Golden rectangles
Earlier, we learned about the Golden Ratio:
\(\varphi=\frac{1+\sqrt{5}}{2}\)
So far, that's all we know. It's an irrational number that has a name and came from the Fibonacci numbers.
Terms
- The Golden Ratio is an irrational number whose name is phi or \(\varphi\) and it is equal to \(\frac{1+\sqrt{5}}{2}\).
- A golden rectangle is any rectangle where the ratio of long side divided by short side is equal to the Golden Ratio.
Examples
Which of these rectangles is golden: a 2 by \(1+\sqrt{5}\) rectangle, a \(\frac{1+\sqrt{5}}{2}\) by 1 rectangle, a 2 by \(\sqrt{5}-1\) rectangle, and a 5 by 2.5 rectangle?
To figure this out, divide the length of the long side by the length of the short side and see if you get the golden ratio. The first rectangle is golden because \(\frac{1+\sqrt{5}}{2}\) is literally the golden ratio. Similarly, in the second rectangle, the long side is \(\varphi\) and the short side is 1, so the ratio must be equal to \(\varphi\). In the third rectangle, notice that
\(\frac{2}{\sqrt{5}-1}=\frac{2}{\sqrt{5}-1}\cdot\frac{\sqrt{5}+1}{\sqrt{5}+1}=\frac{2(\sqrt{5}+1)}{4}=\frac{1+\sqrt{5}}{2}=\varphi\)
So the third rectangle is golden as well. However, the fourth rectangle is not golden, since 5/2.5 is just 2.
Drawing Golden Rectangles
The first lesson here is an art lesson: how can you draw a relatively accurate golden rectangle by hand without a ruler?
Golden Spirals
Next, I do some algebra to show that you can squint really hard and see a golden rectangle as an infinite pile of squares that go around in a spiral shape. Then I draw a spiral in it and it is, in my opinion, very pretty.
Applications of Golden Ratios
One of the most common ways we see Golden Ratio come up is in design, art, and architecture. It is standard advice to art students and photographers to use golden proportions when creating their works. Living artists can be asked if they used the Golden Ratio in their work, and Renaissance artists were prone to leaving clues or visual indications that they used the Ratio; it is debated whether some older works were intentionally designed using the Golden Ratio or if it was unintentional or coincidental. For example, we know that Le Corbusier and other artists from the Staatliches Bauhaus were vocal fans of golden proportions.
Is the golden ratio somehow innate to us? Or is it relatively modern rule invented to determine which art is "attractive?"
Quiz Questions
| Question | Answer |
| 1 | 3 |
| 2 | 2,3 |
| 3 | 4 |
Question 1
What is the definition of a golden rectangle?
- A rectangle where the base is equal to the golden ratio and the height is 1.
- Any rectangle that has perimeter equal to the golden ratio.
- Any rectangle where the ratio of the long side to the short side is equal to the golden ratio.
- A rectangle that is literally made of gold.
- Any rectangle that has area equal to the golden ratio.
Question 2
Which rectangles count as golden rectangles? Select all that apply.
- Base = 1.6, Height = 1
- Base = 100, Height = \(100\varphi\)
- Base = \(1+\sqrt{5}\), Height = 2
- Base = \(\sqrt{5}\), Height = \(\frac{1}{2}\)
Question 3
If we take a golden rectangle which has base equal to \(\varphi\) and height equal to 1, and we subdivide that rectangle into a square and a smaller rectangle using a single vertical edge, what are the dimensions of the smaller rectangle?
- Base .6, Height 1
- Base \(\varphi\), Height 1
- Base \(\frac{\varphi}{2}\), Height \(\frac{1}{2}\)
- Base \(\varphi -1\), Height 1
Homework Questions
Question 3.2.1
A rectangle is golden if the ratio of long side over short side is equal to the Golden Ratio.
Question 3.2.2
\(\frac{5}{3}≈1.67,\frac{6}{4}=1.5,\frac{11}{8.5}≈1.29,\frac{380}{280}≈1.36\). The 3x5 notecard is the closest.
Question 3.2.3
Sure it can. Since the definition says "long over short," there's nothing wrong with the long side being the height.
Question 3.2.4
No they aren't. If the ratio for the original rectangle is \(\frac{a}{b}=\varphi\), then the ratios for the halves has to be \(\frac{a}{.5b}=2\varphi\).
Question 3.2.5
Yes, they are. Both the long side and the short side are divided in half, so when you put them in a fraction, you still get the Golden Ratio.
Question 3.2.6
Reflection question. Responses vary.
Question 3.2.1
Explain what makes a rectangle a Golden rectangle.
Question 3.2.2
Which of the following objects is closest to being a Golden rectangle? An 8.5x11 inch sheet of paper, a 3x5 inch index card, a 4x6 inch index card, or the state of Colorado (380 miles by 280 miles)?
Question 3.2.3
Can a Golden rectangle have a shorter base than height? Why or why not?
Question 3.2.4
Suppose you have a Golden Rectangle made out of paper and you fold it in half along its short side, so the fold is parallel to the longer side. Are the two halves Golden rectangles? Why or why not?
Question 3.2.5
Suppose you have a Golden Rectangle made out of paper and you fold it in half along its base and then in half along its height. Are the four smaller rectangles Golden rectangles? Why or why not?
Question 3.2.6
Reflection question: what does it mean to understand a concept? What is a concept that you went from not understanding to understanding recently?