3.3 Platonic solids

Overview
| TCCNS Course | MATH 1332: Contemporary Mathematics |
| UT Austin Course | M 302: Introduction to Mathematics |
Introduction
Suggested Resources and Preparation
Materials and Technology
For the instructor: Magnetic tiles are immensely helpful for demonstrating why there are only five regular solids. Alternately, students can attempt to use paper polygons or build models using strawn and pipe cleaners.
Prerequisite Assumptions
- It can help to remember how to find the interior angles of regular polygons, but it is not necessary.
Overview and Student Objectives
Lesson Length
50 minutes
Lesson Objectives
Students will understand that:
- There are infinitely many regular polygons, but there are only five regular solids.
- We can more easily count the features (vertices, edges, and faces) of polyhedra by imagining the faces disassembled first, counting their features, and then dividing by 2, 3, 4, or 5, depending on how the solid is assembled.
Students will be able to:
- Define a regular polygon and a regular solid.
- Name and describe (or draw) the five regular solids.
Platonic solids
Terms
- A polygon is a two-dimensional shape with straight sides or edges.
- A regular polygon is a polygon where each side has equal length and all interior angles are equal.
- A regular solid/Platonic solid/regular polyhedron is a three-dimensional solid whose faces are all matching regular polygons and where the same number of faces meet at each vertex.
https://utexas.hosted.panopto.com/Panopto/Pages/Viewer.aspx?id=ad75ba93-4508-497f-81c0-ac08003d6a18
Meet the regular solids
There are infinitely many regular polygons. Just choose how many sides you want, then arrange them in a circular shape so that all interior angles match. Here are a few:
On the other hand, there are only five regular solids:
Counting regular polygons and regular solids
Counting features of regular solids
In order to count the vertices and edges of regular solids, you either need a set of solids (and if you are a gamer, this is a great time to break out those polyhedral dice), or you need a technique for doing the counting on paper. These formulas can help you on homework.
How to count vertices/edges of solids
- Vertices of solid: take the number of faces times the number of vertices per face and then divide by the number of faces that meet up at each vertex.
- Edges of solid: take the number of faces times the number of edges per face and then divide by 2.
Proof that there are only five regular solids
This video walks you through a proof by cases that there are only five regular solids. First, you choose which kind of polygon you want to build out of. There are only three that work at all: triangles, squares, pentagons. Then you choose how many of these polygons you want to meet at each vertex. By attempting each case systematically, you find out that only five regular solids are possible.
Proof of only five regular solids
Quiz Questions
| Question | Answer |
| 1 | 3 |
| 2 | 3 |
| Object | Vertices | Edges | Faces |
|---|---|---|---|
| Tetrahedron | 4 | 6 | 4 |
| Cube | 8 | 12 | 6 |
| Octahedron | 6 | 12 | 8 |
| Dodecahedron | 20 | 30 | 12 |
| Icosahedron | 12 | 30 | 20 |
Question 1
What is the definition of a regular solid?
- A solid is regular if all faces are matching regular polygons.
- A solid is regular if all faces are polygons and if there's an even number of vertices.
- A solid is regular if all faces are matching regular polygons and if the same number of faces join at each vertex.
- A solid is regular if all faces are regular polygons and if the same number of faces join at each vertex.
- A solid is regular if it has perfect symmetry from all angles.
Question 2
How many regular solids are there?
- Infinitely many
- Three
- Five
- None
Question 3
Complete this chart showing the numbers of vertices, edges, and faces of each Platonic solid.
| Object | Vertices | Edges | Faces |
|---|---|---|---|
| Tetrahedron | |||
| Cube | |||
| Octahedron | |||
| Dodecahedron | |||
| Icosahedron |
Homework Questions
Question 3.3.1
A polygon is a regular polygon if all sides are the same length and all interior angles are equal. Drawn responses may vary.
Question 3.3.2
A solid is regular solid if it is a polyhedron, meaning that all faces are flat polygons, and if all faces are matching regular polygons, and if the same number of polygons come together at each vertex.
Question 3.3.3
Drawings vary. Check for the right types of polygons and that the correct number are meeting up at each vertex. Proportions are less important.
Question 3.3.4
Tetra: 4-6+4=2
Cube: 8-12+6=2
Octa: 6-12+8=2
Dodeca: 20-30+12=2
Icosa: 12-30+20=2
Question 3.3.5
There are 12 pentagons and 20 hexagons. Three shapes meet up at each vertex. So there are a total of 32 faces, \(\frac{12×5+20×6}{2}=90\) edges and \(\frac{12×5+20×6}{3}=60\) edges. Then we get 32-90+60=2.
Question 3.3.6
You get a cuboctahedron.
Question 3.3.7
You get 48/4=12 vertices, 48/2=24 edges, and 14 faces. You get 12-24+14=2.
Question 3.3.8
Reflection essay. Responses vary.
Question 3.3.1
When is a polygon a regular polygon? Draw four different regular polygons and four different non-regular polygons.
Question 3.3.2
What makes a solid a regular or Platonic solid?
Question 3.3.3
Draw the five regular solids by hand. This can be challenging, but just do your best. Try to make sure your solids are "mathematically correct" even if they are a little floppy or crooked.
Question 3.3.4
For each of the regular solids, take the number of vertices, subtract the number of edges, and add the number of faces. What do you get?
Question 3.3.5
There's a family called the Archimedean solids. You still have the same number of polygons coming together at each vertex, and you still have all faces being regular polygons, but they don't all have to match.
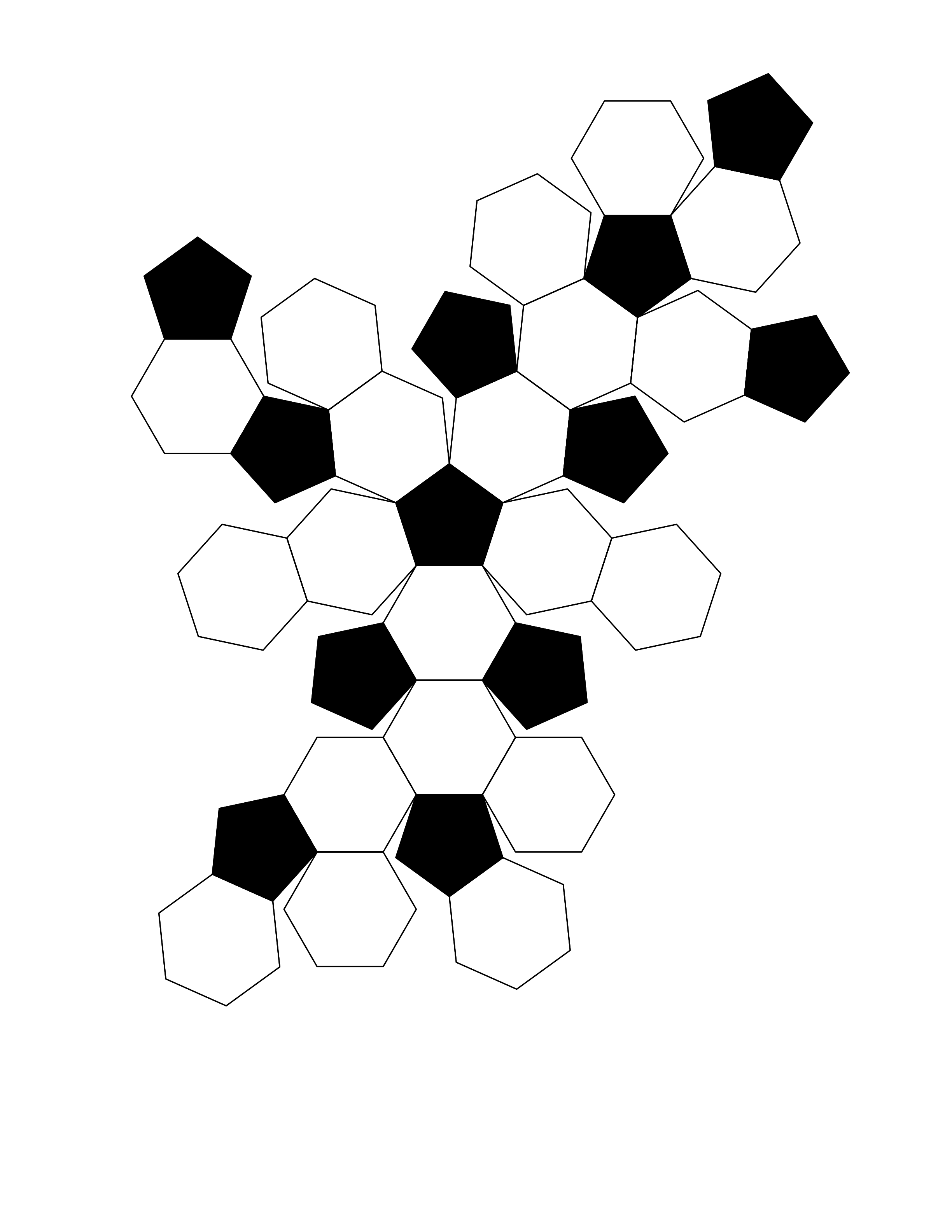
Think of a soccer ball as a polyhedron (with flat faces).
Count the number of vertices, edges, and faces. Next, take the number of vertices, subtract the number of edges, and add the number of faces. What do you get? This cut-open soccer ball, or net, may be helpful.
Question 3.3.6
Draw a solid made out of eight equilateral triangle faces and six square faces. At each vertex you have two triangles and two squares meeting up in an alternating pattern. You need to (try to) draw the actual 3D solid. Here is the net:
Question 3.3.7
For the solid in Question 6, count the number of vertices, edges, and faces in this solid. Then calculate V−E+F.
Question 3.3.8
Choose an essay or project that you did, recently or a skill that you have (this is purposely very broad). Choose something you think you do or did well. But there's always room for improvement!
- Briefly describe the essay, problem, or skill (one or two sentences)
- Give some examples of why you think your work or skill is good (one or two sentences), and then
- Describe at least two ways in which you think you could improve even more (one or two paragraphs, at least 100 words).
This activity is much more challenging than it might first appear. If you are stuck, ask a friend or teacher or coach for ideas. Honest self-reflection and self-evaluation is crucial for progress, no matter what you are into.