- Author:
- Amanda Hager
- Subject:
- Mathematics
- Material Type:
- Lesson
- Level:
- Academic Lower Division
- Provider:
- University of Texas at Austin
- Tags:
- License:
- Creative Commons Attribution
- Language:
- English
- Media Formats:
- Text/HTML, Video
3.1 Pythagorean Theorem

Overview
| TCCNS Course | MATH 1332: Contemporary Mathematics |
| UT Austin Course | M 302: Introduction to Mathematics |
Introduction
Suggested Resources and Preparation
Materials and Technology
For the instructor: Kits of four triangles and a square (attached) may be useful for getting the students to visualize certain proofs of the Pythagorean Theorem
Using some sort of rectangular frame, say using popsicle sticks and brads/thumbtacks, or boards that can be screwed together using butt joints, can help immensely in convincing students that the Pythagorean Theorem lets one get a much more exact angle than eyeballing or using a carpenter's square. A tape measure is required.
Prerequisite Assumptions
- Students should be able to solve equations using sums, differences, and squares of real numbers using a calculator.
Overview and Student Objectives
Note: this lesson is designed to give a fresh perspective on the Pythagorean Theorem to students who have already been exposed to the topic and have solved triangles before.
Lesson Length
50 minutes
Lesson Objectives
Students will understand that:
- The Pythagorean Theorem is not just for solving triangles - there is a 90 degree angle in a triangle if and only if the Pythagorean equation is true.
- In order for three side lengths to form a triangle, the longest side must be shorter than the sum of the lengths of the shorter two sides.
Students will be able to:
- Solve for the third side of a right triangle given the side lengths of the other two sides.
- Determine if a triangle has a 90 degree angle in it based on the side lengths alone.
- Describe how the Pythagorean Theorem may be used in applications such as construction to ensure that an angle is 90 degrees.
- Prove that the Pythagorean Theorem is true by manipulating paper copies of a right triangle and/or drawing diagrams.
Pythagorean Theorem
Pythagorean Theorem
If a, b, and c represent the lengths of sides of a triangle, then:
a2+b2=c2 if and only if the triangle is a right triangle.
Algebra skills review
Before we get started, you need to review the basics of using Pythagorean Theorem the way we typically teach it in American high schools. I recommend this short example-based tutorial from Khan Academy.
They also provide sets of practice problems you can try.
Proving the Pythagorean Theorem
The math that isn't typically taught in high school, however, is the proof of why the Pythagorean Theorem works the say that it does. There are actually many, many proofs of this theorem, over 300. We credit Pythagoras (c. 560 - c. 480 BCE), but the theorem has been discovered on a Babylonian tablet going back to 1900 - 1600 BCE.1 We also have evidence that the Egyptians knew this theorem as well and used it when building.

A couple other more famous people "own" proofs of the Theorem. Leonardo Da Vinci's proof is popular, but my favorite one might be President James A. Garfield, who was a lawyer, not a mathematician, and published his proof while working Congress four years before being elected president.
I'm asking you to study three different proofs of the theorem: Bhaskara's Proof, Da Vinci's Proof, and what I'm calling the Big Square Proof.
https://utexas.hosted.panopto.com/Panopto/Pages/Viewer.aspx?id=80158b6f-12ad-43dd-abe1-ac080038a28a
https://utexas.hosted.panopto.com/Panopto/Pages/Viewer.aspx?id=22688bbf-36bc-46aa-824f-ac080038a2ba
https://utexas.hosted.panopto.com/Panopto/Pages/Viewer.aspx?id=ad0f616a-3266-4302-b1ca-ac080038a2ec
Pythagorean Theorem in Action
A little-remembered fact about the Pythagorean Theorem is that it's reversible. Everybody knows that if you have a right triangle, then \(a^2+b^2=c^2\). But it turns out that if you have any triangle at all, and you measure and find out that \(a^2+b^2=c^2\), then you can say there's a right angle.
This is really important for building things that aren't awful. You'd think you could just use a carpenter's square or the edge of a ruler or something to make sure what you're building has nice right angles, but there will usually be pretty big errors that compound later and make your project look like garbage. So there's a little trick using a tape measure that helps you get perfect right angles every time. Just measure 3 feet (or inches or meters or centimeters, doesn't matter) along one edge and measure 4 feet along the other edge from a corner. If the distance between those two points is 5 feet, you have a perfect right angle!
References
1Pythagorean Theorem, from cut-the-knot.org.
Quiz Questions
| Question | Answer |
|---|---|
| 1 | 2 |
| 2 | 4 |
| 3 | 3 |
| 4 | 3 |
| 5 | 3 |
Question 1
In a right triangle with legs of lengths 6 and 8, what is the length of its hypotenuse?
- length is 14
- length is 10
- length is 100
- length is 48
Question 2
If the hypotenuse of a right triangle has length 13 and one of its legs has length 5, what is the length of the other leg?
- length is 144
- length is 18
- length is 8
- length is 12
Question 3
In Bhaskara's proof of the Pythagorean Theorem, a square is constructed whose sides are of length equal to the hypotenuse of the right triangle. Four copies of the right triangle are used to make that square plus there is an additional square in the middle to fill in the square on the hypotenuse. If the longer leg of the original right triangle has length b and the shorter leg has length a, what is the length of each side of that little square in the middle?
- c
- a
- b-a
- It's impossible to say.
- It depends
Question 4
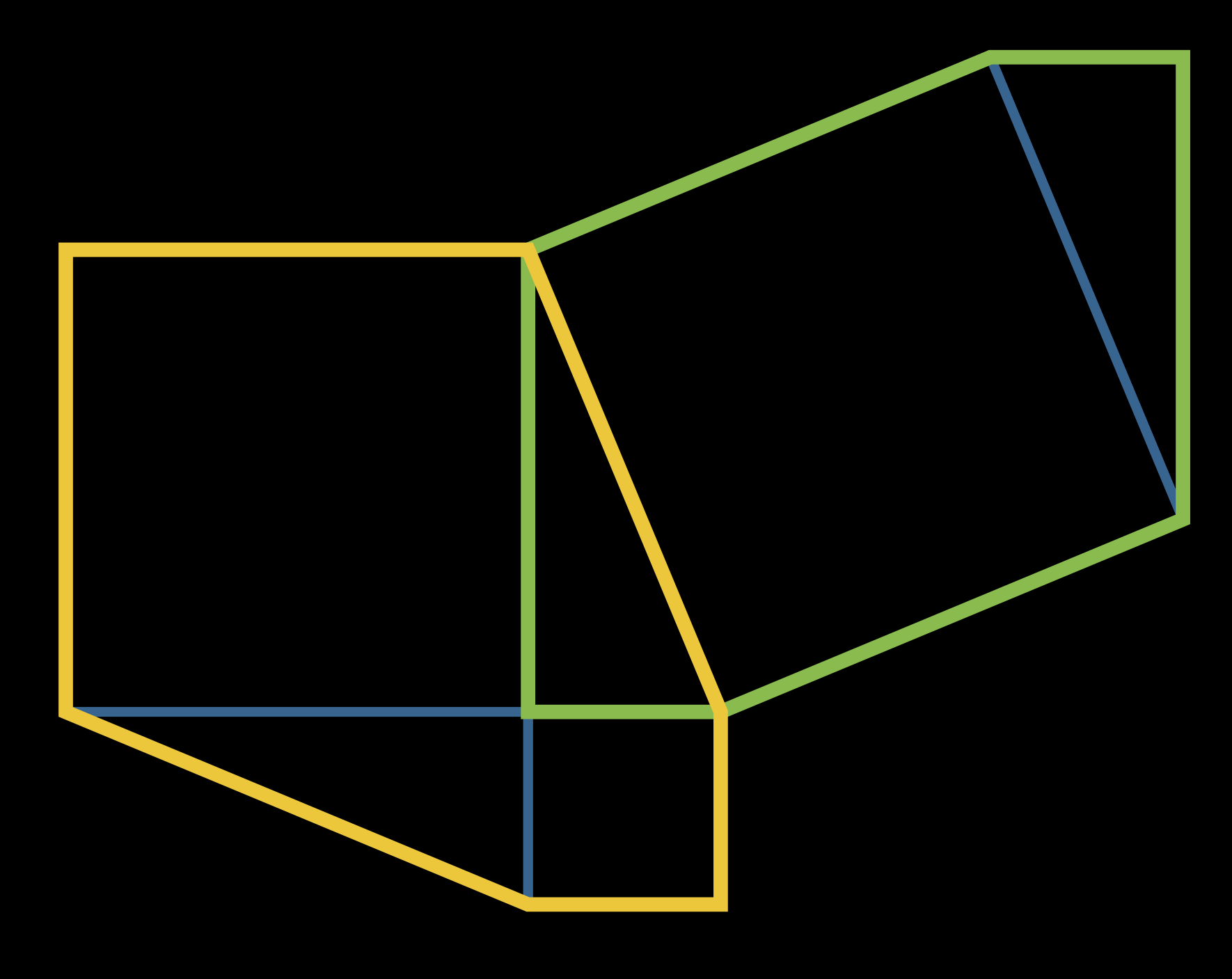
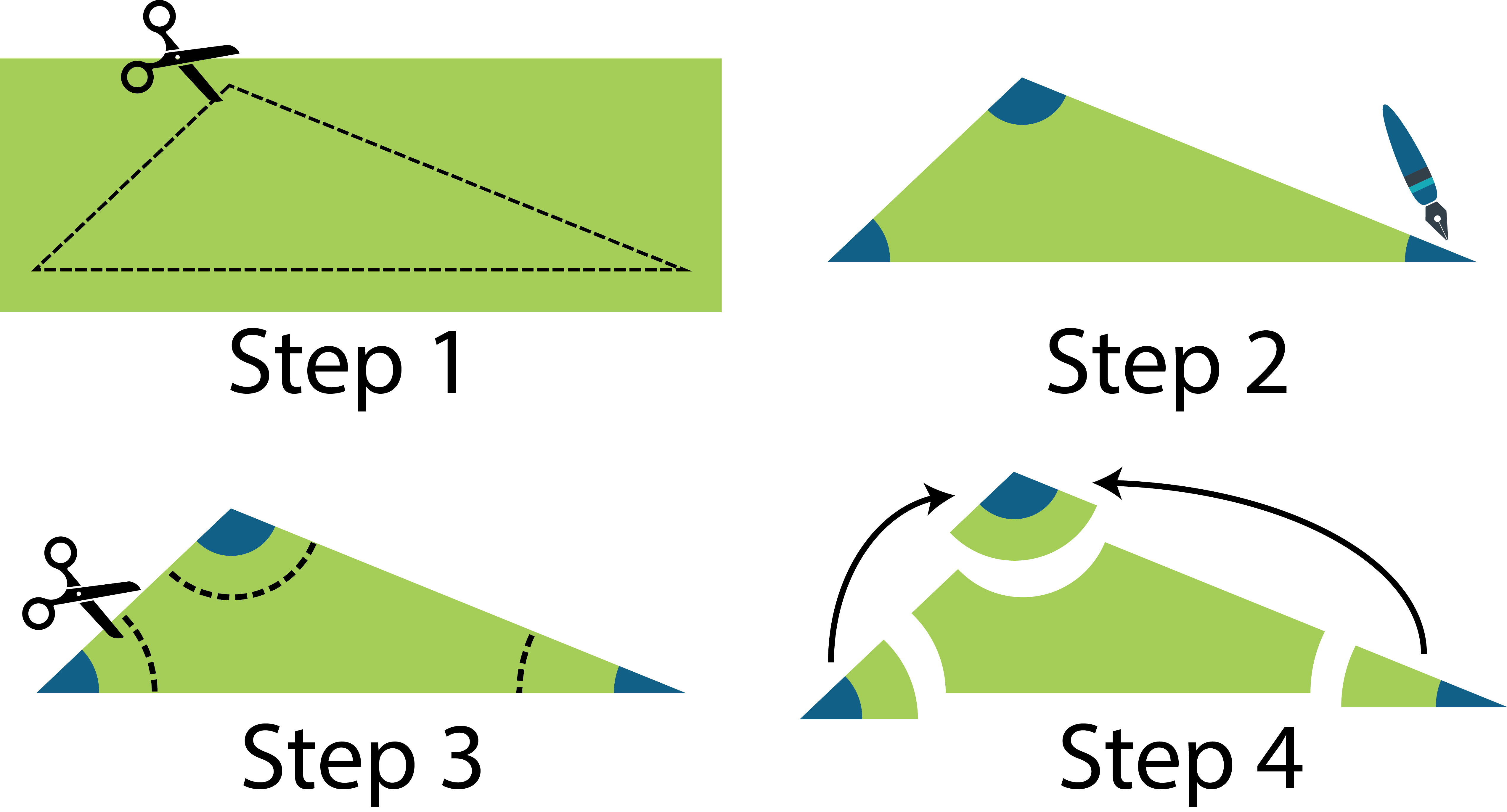
Suppose you have a right triangle with legs of lengths a and b and hypotenuse of length c. Suppose you put four copies of the right triangle into the four corners of a square whose side lengths are a + b as was done in the Big Square proof of the Pythagorean Theorem. How do you know that the shape in the center will be a perfect square?
- Because all sides of the shape are equal to c, and anytime that happens, we know the shape will be a square.
- If the outer shape is a square, then the inner shape has to be a square too.
- The sum of the two non-right angles of a right triangle is 90 degrees since the sum of all the angles of any triangle is 180 degrees. So since at each vertex both of the smaller angles of the right triangle appear and since a straight angle has 180 degrees, then each angle of the shape must be 90 degrees. All sides are equal, so it must be a square.
- It just happened by accident in this case.
Question 5
In Leonardo da Vinci's proof of the Pythagorean Theorem, he showed that the areas of two 6-sided figures are the same. Why does that prove the Pythagorean Theorem?
- It proved the Pythagorean Theorem because the two six-sided shapes overlap a little bit, and that overlap is the triangle.
- It doesn't actually prove the Pythagorean Theorem because we were supposed to make the small square plus the medium square equal to the big square in area.
- In one case the 6-sided figure had area equal to the area of two copies of the right triangle plus the sum of the squares on the two legs whereas the other, equal area 6-sided figure had area equal to the area of two copies of the right triangle plus the area of a square on the hypotenuse. So subtracting the areas of two copies of the right triangle from each showed that the sum of the squares of the two legs equals the square on the hypotenuse.
- It shows the Pythagorean Theorem because it shows that \(a^2+b^2=c^2\).
Homework Questions
Question 3.1.1
A right triangle with legs of length 2 and 3 has hypotenuse \(\sqrt{3^2+2^2}=\sqrt{13}\). A triangle with hypotenuse 7 and leg 3 has other leg \(\sqrt{7^2-3^2}=\sqrt{40}\). Simplified and decimal responses are also acceptable, for example \(\sqrt{40}=2\sqrt{10}\approx6.32\).
Question 2
Question 3.1.3
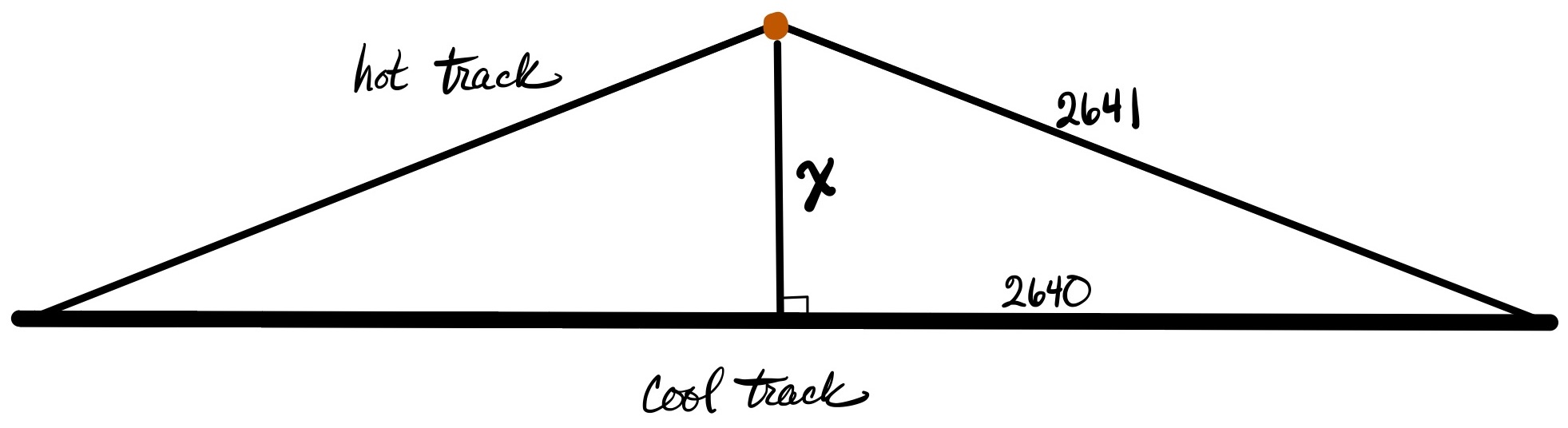
So the track buckles straight upward and creates two back-to-back right triangles. The bottom edge overall is 1 mile or 5280 feet, so the bottom edge of one right triangle is 2640. The heated track is 5282 feet long, so the hypotenuses of each triangle are half that or 2641 feet. This means that the last leg must be equal to \(\sqrt{2641^2−2640^2}=\sqrt{5281}≈73\) feet. Format of answer doesn't matter.
Question 3.1.4
No because \(5^2+5^2\neq12^2\).
Question 3.1.5
No because \(5+5<12\).
Question 3.1.6
Measure out 3 units on one string and 4 units on the other string, then measure the distance between points. If the distance is exactly 5 feet, you have a 90 degree angle.
Question 3.1.7
Mindset questions. Responses vary.
Question 3.1.1
If a right triangle has legs of length 2 and 3, how long is the hypotenuse? If a different right triangle has a hypotenuse of 7 and a leg of length 3, how long is the other leg?
Question 3.1.2
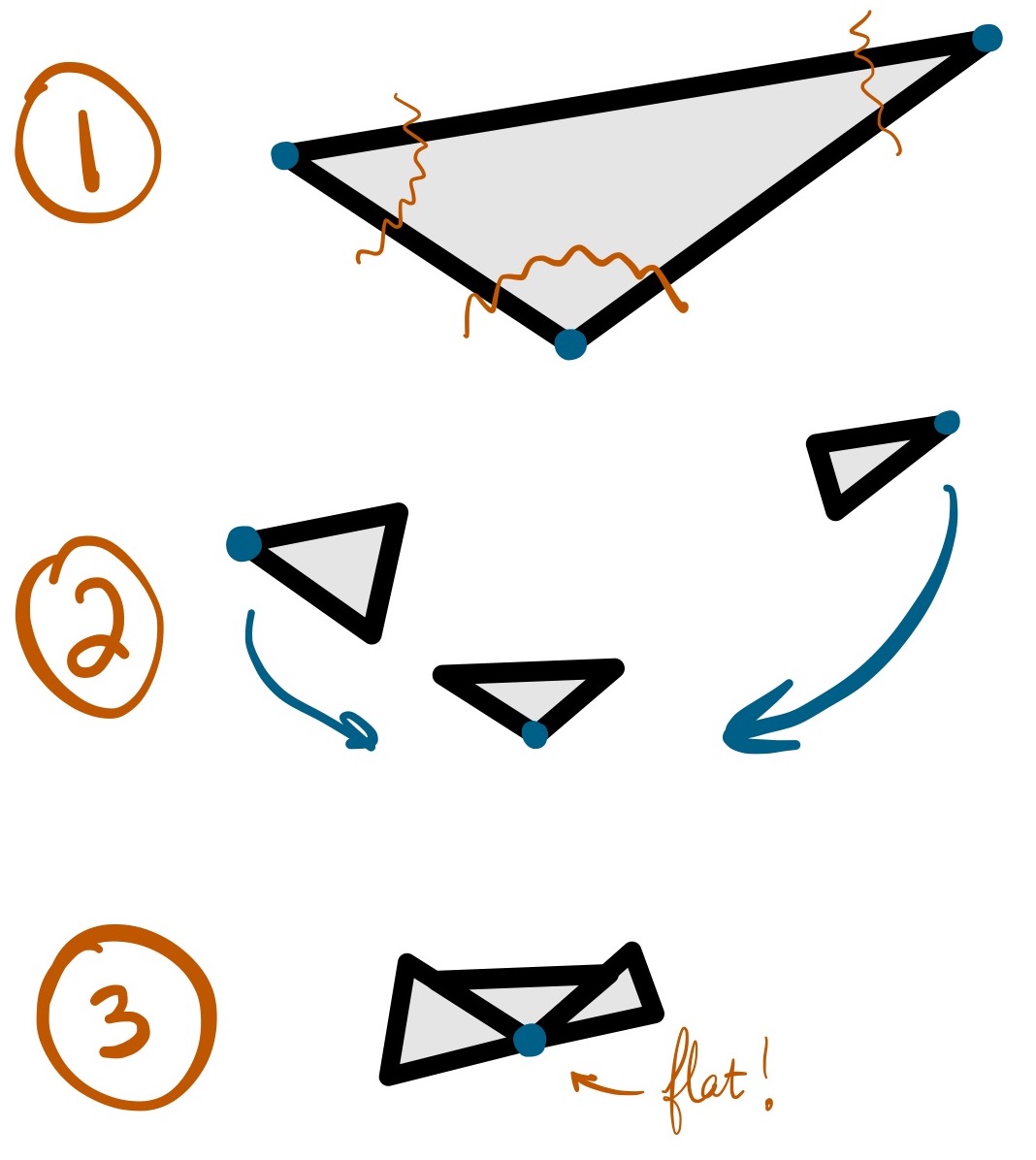
Draw a random triangle, using a straightedge so it's more accurate. Cut it out with scissors. Mark each of the three corners with a dot or arrow. Then cut the corners of the triangle off and push them together so the dots touch.
- Describe or show what you get (you are welcome to embed a photo if you like).
- What do you conclude about the angles of a triangle?
Question 3.1.3
Train tracks are made of metal. Consequently, they expand when it's warm and shrink when it's cold. When riding in a train, you hear the clickety-clack of the wheels going over small gaps left in the tracks to allow for this expansion. Suppose you were a beginner at laying railroad tracks and forgot to put in the expansion gaps. Instead, you made a track 1 mile long that was firmly fixed at each end. On a hot day, suppose the track expanded by 2 feet and buckled upward. Assume that the track forms an isosceles triangle with the highest point in the middle. Roughly how high would the midpoint be?
Question 3.1.4
Can there be a right triangle with sides equal to 5, 5, and 12?
Question 3.1.5
Can there be any kind of triangle with sides equal to 5, 5, and 12?
Question 3.1.6
When building fences or patios, people often use strings to lay out the shape before digging. Here is an example of a building foundation being laid out using string:
It is important to get the strings to meet in 90 degree angles.
The secret to using batterboards and strings is that the strings can be wiggled left or right until the shape is exactly the way you want it. An old trick is to use the Pythagorean Theorem and tape measure to make sure the corners are 90 degrees.
How does this work?
Question 3.1.7
Sometimes we can best test our own understanding by trying explain what we know to someone else. Your task is to explain one proof of the Pythagorean Theorem to someone in your life who is not in this class. Answer the following questions:
- Who did you explain the proof to?
- What was their reaction?
- Do you feel confident in your explanation? Why or why not?
- If you had to do the assignment a second time, what would you do differently?