4.2 Four special surfaces

Overview
| TCCNS Course | MATH 1332: Contemporary Mathematics |
| UT Austin Course | M 302: Introduction to Mathematics |
Introduction
Suggested Resources and Preparation
Materials and Technology
For the instructor: 1" wide strips of construction paper, scissors, tape to create Möbius bands and annuluses.
Prerequisite Assumptions
Students need to be familiar with the concepts of dimension and boundary as they are presented in Section 3.4.
Overview and Student Objectives
Lesson Length
50 minutes
Lesson Objectives
Students will understand that:
- Some 2D surfaces are orientable and some are non-orientable.
- Identification diagrams are a technique we use to work with a object in space by flattening it out on paper (like a map of the globe).
Students will be able to:
- Describe how four different kinds of identification diagrams create the annulus, Möbius band, torus, and Klein bottle.
- Perform experiments on Möbius bands made of paper by cutting or marking on them, documenting their results and making conjectures about mathematical properties.
- Determine whether or not an object has edges or is orientable using its identification diagram.
Four special surfaces
Annulus and Möbius Band
Terms
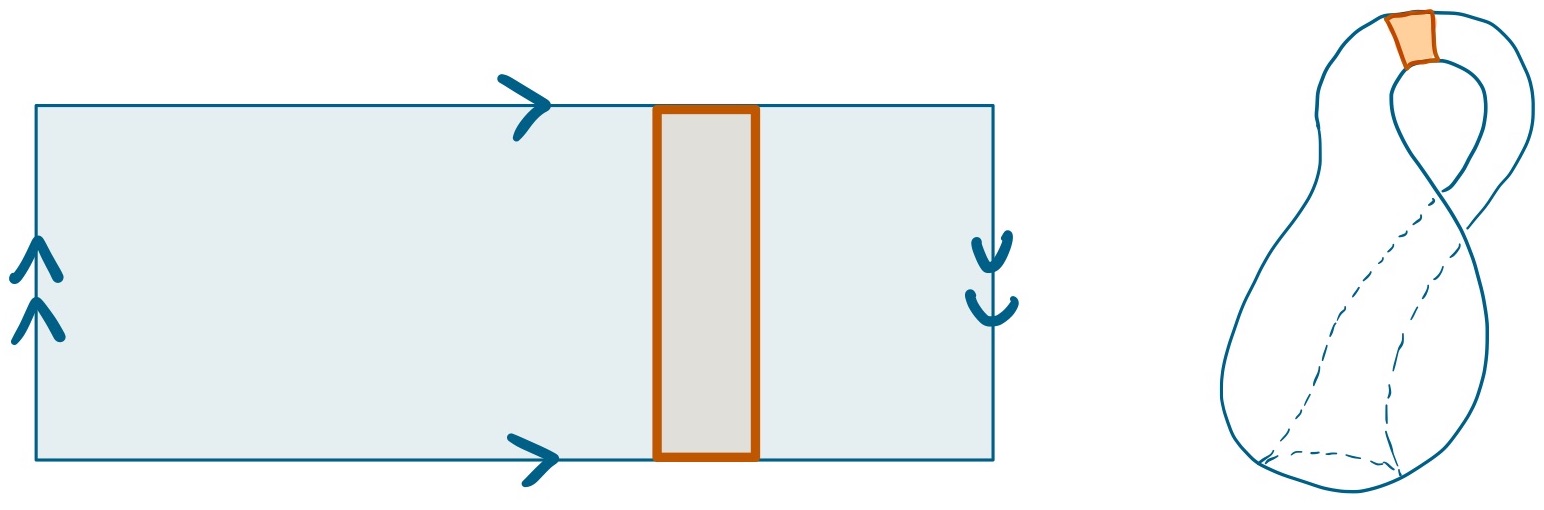
An annulus is a 2-D surface that is ring-shaped. You can make one by taking the short ends of a rectangle and attaching them without any twists. You can also think of it as a thin toilet-paper tube, or a cylinder with no top and no bottom.
A Möbius band is a 2-D surface that you get by taking the short ends of a rectangle and attaching them with a half-twist.
Image credit: David Benbennick.
What are identification diagrams?
Terms
An identification diagram (sometimes called an edge identification diagram) is a 2-D picture that shows how to assemble a surface by attaching edges to each other. Different types of arrows are used to differentiate between pairs of edges. Diagrams can start with rectangles, hexagons, or any other flat shape.
Torus and Klein Bottle
Terms
A torus is a 2-D object that looks like a hollow donut.
A Klein bottle is a 2-D object that you can create from a rectangle by attaching one pair of opposite edges without twisting, then attaching the other pair of edges with a half-twist.
TL;DR
| Shape | No. of dimensions | No. of boundary pieces | No. of "sides" | Identification Diagram |
| Annulus | 2 | 2 | 2 |  |
| Möbius band | 2 | 1 | 1 |  |
| Torus | 2 | 0 | 2 |  |
| Klein bottle | 2 | 0 | 1 |  |
Quiz Questions
Question 1
4
Question 2
1, 1, 2, 2
Question 3
1, 2
Question 4
2
Question 1
What is a Möbius band?
- It is any strip of paper with the ends glued together.
- Any strip of paper with arrows on it that tell you how they attach.
- It is a heavy metal band from the 80s.
- It is a 2D object that you can make out of a rectangle by putting in a half twist and gluing two ends together.
Question 2
Fill in the blanks: A Möbius band has ____ side(s) and ____ edge(s). An annulus has ____ sides(s) and ____ edge(s).
Question 3
Fill in the blanks: If you cut a Möbius band one third of the way from the edge and keep cutting, you get ____ piece(s). If you cut an annulus one third of the way from the edge and keep cutting as long as possible, you get ____ piece(s).
Question 4
Your sister holds a strip of paper. She gives one end a half twist, then she gives the other end a half twist in the same direction, then she tapes the ends together. Does she get a Möbius strip?
- Yes
- No
- Impossible to determine.
- It depends.
Homework Questions
Question 4.2.1
You can trace an edge with a finger, or you can trace the surface of the paper. If there's one edge, or if your finger is on the other side of the paper after one trip around, then it's a Möbius band.
Question 4.2.2
You do not. The resulting object has two sides and two edges, so it can't be a Möbius band.
Question 4.2.3
You get two copies of the same object but they're interlinked. These objects are not quite annuluses but they're not Möbius bands either. But they are orientable, meaning they have two sides and two edges.
Question 4.2.4
No. If you hold the strips together and try to keep them that way as you build a Möbius band, you find that you have to choose to assemble one or the other. You can't tape both.
If we are putting the ends of the strips together without twisting, however, we see that the same-colored edges meet up. Two pieces of tape later and we have a pair of annuluses.
Question 4.2.5
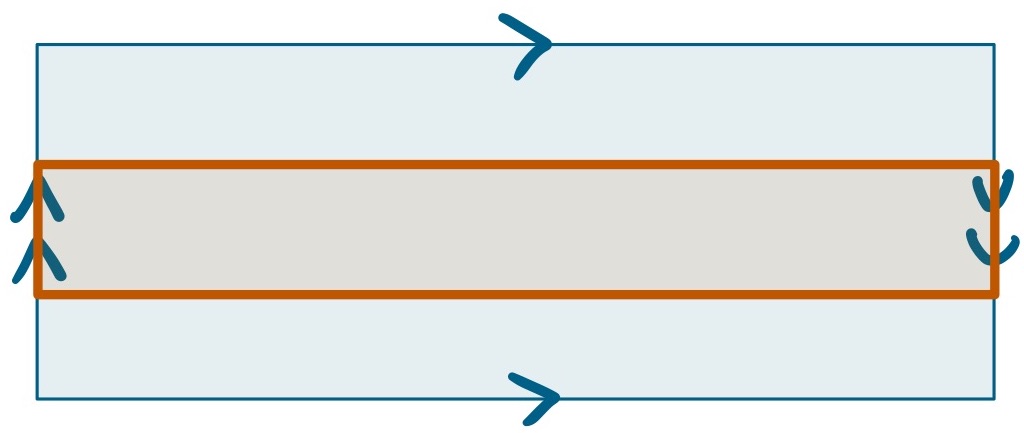
This diagram is similar to the one for the Klein bottle. Students should draw a rectangle with two edges identified in opposite directions, and two edges left alone. If the left and right edges are identified, then draw a horizontal thin rectangle down the center of the object. That rectangle will be a Möbius band.
Question 4.2.6
Question 4.2.7
Question 4.2.8
Reflective writing prompt. Responses vary.
Question 4.2.1
Give two different techniques for looking at a loop of paper and determining if it is a Möbius band.
Question 4.2.2
Take a strip of paper, give one end two half-twists, and tape the ends. Do you get a Möbius band? Why or why not? (Hint: trace with your finger and count how many edges it has).
Question 4.2.3
Take a strip of paper, put two half-twists in it, and tape the ends together (you can use the same strip from problem 2). Then cut the paper along its midline all the way around. What do you get? Can you explain why you get that?
Question 4.2.4
Hold two differently-colored strips of paper together, say white and blue, then give them a half-twist. Are you able to connect white to white and blue to blue? Is the answer different if you try to keep the pieces of paper together and create annuluses with them?
Question 4.2.5
Show on an identification diagram that when you cut a Möbius band all the way around 1/3 of the way from the edge, that the middle section of the Möbius band is still a Möbius band.
Question 4.2.6
Prove that you can make two cuts in a Klein bottle and cut out an annulus. Draw a Klein bottle and show the cuts on the Klein bottle, then show an identification diagram for a Klein bottle and show the two cuts there.
Question 4.2.7
Prove that you can make one cut in a Klein bottle and cut out a Möbius band. (Hint: it should probably be perpendicular to the cuts in Question 4.2.6.
Question 4.2.8
Reflect on today, the day you are completing this assignment. Write down three things you did, said, or learned that made you feel proud. Why are you proud that you did, said, or learned these things?