4.4 Torus Knots

Overview
| TCCNS Course | MATH 1332: Contemporary Mathematics |
| UT Austin Course | M 302: Introduction to Mathematics |
Introduction
Overview and Student Objectives
Lesson Length: 40-45 minutes
Overview: Torus knots provide a nice class of knots which we can study in several different ways. In this lesson we'll introduce these knots and explain how an identification diagram can be used to gather geometric information about them.
Lesson Objectives:
Students will understand that:
- Certain knots can be viewed as curves on a torus;
- Geometric information is meaningfully stored in the identification diagram and;
- Different representations of the same object have value.
Students will be able to:
- Recognize closed curves on the identification diagram of a torus and;
- Use identification diagrams to describe the shape of a torus knot.
Suggested Resources and Preparation
Materials and Technology:
The interactive torus knot generator, where Part I is used in lecture while Part II is reserved for the homework. This can be accessed from mobile devices.
Prerequisite Assumptions: Students should be familiar with identification diagrams as presented in Section 4.2: Four Special Surfaces. They will also need to be familiar with terms and practices from Section 4.3: Knot Theory.
Suggested Instructional Plan
Frame the Activity (5 minutes)
- Ask students to think of kinds of knots they know. How many can they come up with? Remind them of knots they've studied -- the unknot, trefoil etc.
- Lead them to torus knots by acknowledging the difficulty in generating new knots. The torus knots provide a nice set of knots which can be easily described and studied.
Activity Flow (30 minutes)
- Instructor is advised to follow the body as presented in subsequent sections. Italicized questions provide opportunities for student engagement.
- Use the knot generator (linked above) to provide demonstrations in real-time.
Wrap-up/Transition (5-10 minutes)
- Explain the importance of different representations of the same object, as summarized in the "Thinking Mathematically" section.
- Time permitting discuss quiz questions with students. Otherwise, Question 1 may be used as an exit slip.
Overview
Torus knots provide a nice class of knots which we can study in several different ways. In this lesson we'll introduce these knots and explain how an identification diagram can be used to gather geometric information about them.
Lesson Objectives
You will understand that:
- Certain knots can be viewed as curves on a torus;
- Geometric information is meaningfully stored in the identification diagram and;
- Different representations of the same object have value.
You will be able to:
- Recognize closed curves on the identification diagram of a torus and;
- Use identification diagrams to describe the shape of a torus knot.
Materials and Technology
The interactive torus knot generator, where Part I is used in lecture while Part II is reserved for the homework. This can be accessed from mobile devices.
Torus Knots
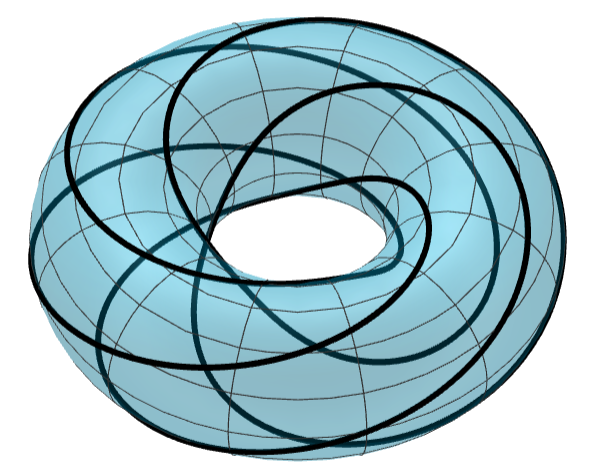
Imagine a torus (depicted in blue below), and drawing on it with a pencil. This creates a curve on our torus. If you finish drawing where you started, we say it is a closed curve. While these curves in general can be very intricate and complicated, many of the knots we've encountered in class can actually be described as curves on a torus (depicted in black below) -- we call these torus knots.
Lines on Identification Diagrams
Remember that we can portray the torus via the following identification diagram:

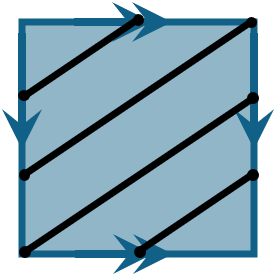
Imagine starting at the bottom-left corner of the diagram and tracing a straight line with slope \(3/2\).
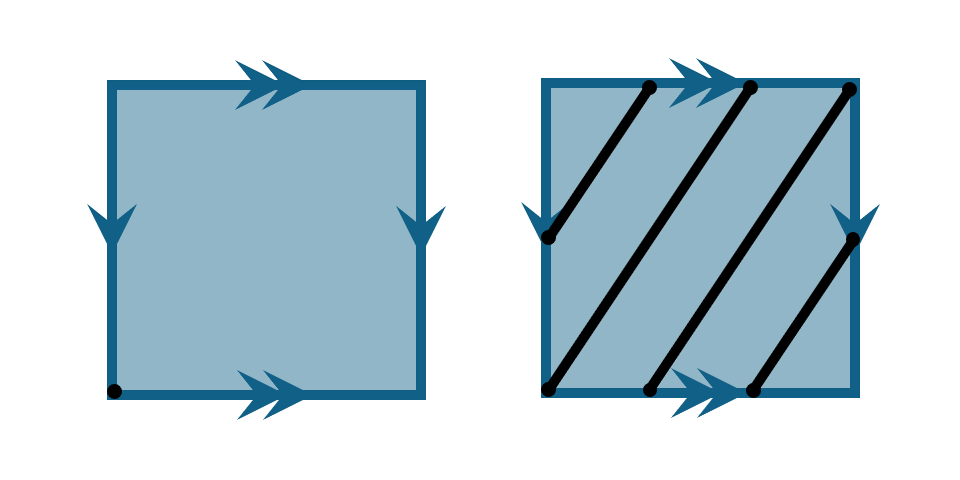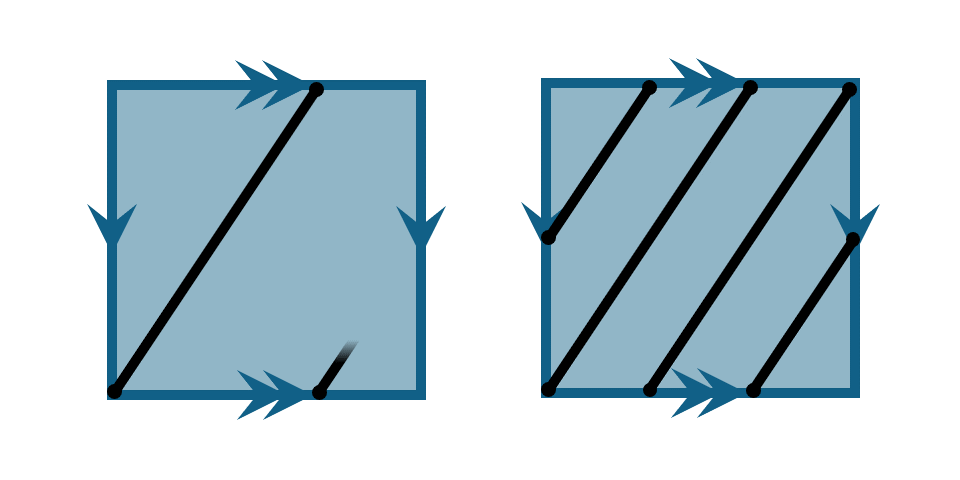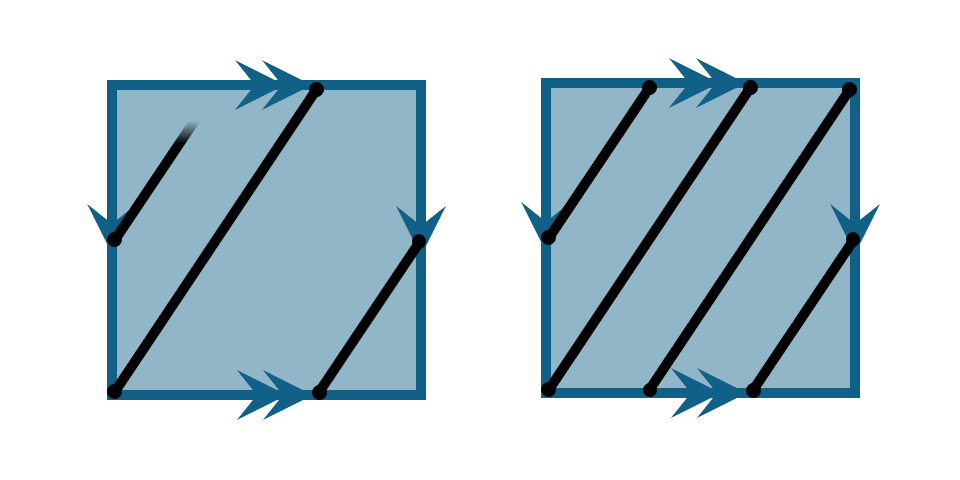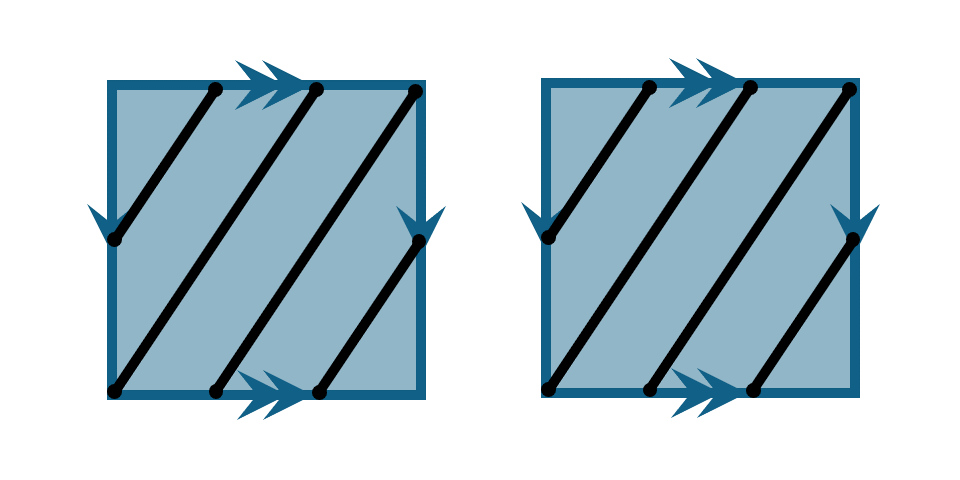
Notice that whenever we reach the boundary of the square we must use the identification to continue drawing.
Question: Is this a closed curve?
Yes, it is! Even though we're drawing a straight line, it is still a type of curve. Since we end up back at the beginning, it is a closed curve. Currently this may be a little hard to see, but if we draw the torus in its usual donut shape we get the following:

Question: What kind of knot have we drawn?
We've just drawn the trefoil knot!
Terms
- A curve is any path in space. Sometimes these can be confined to the surface of an object, for example the torus.
- A closed curve is a curve which ends where it started.
- A torus knot is a closed curve on the surface of a torus.
Changing the Slope
Open now the interactive torus knot generator (Links to an external site) to supplement our discussion and navigate to Part 1. It should currently display a trefoil, with the \(n\) slider set to \(3\) and the \(d\) slider set to \(2\).
Now what will happen if we start changing the original slope we used, from \(3/2\) to a different rational number? Let's call the numerator of the slope \(n\) and the denominator \(d\), so that we're always drawing a line with slope \(n/d\). To generate the trefoil, we had \(n=3\) and \(d=2\).
In the Geogebra applet, set the \(n\) and d sliders both to \(1\). By clicking and dragging on the torus, rotate it so you are looking from a top-down perspective.
Question: By increasing the \(n\) slider, how does the knot change? For example, how does the number of "petals" change?
Notice that the number of "petals" is equal to the number \(n\) that we choose, and as we travel around the petal we move from the bottom of the torus to the top.
Once more set the \(n\) and \(d\) sliders to \(1\) and view the torus with a top-down perspective.
Question: By increasing the \(d\) slider, how does the knot change? For example, how many loops does it form around the central hole?
Notice that the number of "loops" is equal to the number \(d\) that we choose, and each loop winds around the central hole of the torus.
This investigation suggests the numbers \(n\) and \(d\) control the shape of the knot in a predictable way. Specifically, the number \(n\) (the numerator of the slope) is telling us how many times the knot goes from the bottom of the torus to the top. On the other hand, the number \(d\) (the denominator of the slope) is telling us how many times the knot goes around the torus. How can we tell for sure though?
Let's start by analyzing the identification diagram with slope \(3/2\). Notice if we travel along a horizontal edge (where one of the gluings occurs), the line intersects at exactly \(3\) points. On a vertical edge (where the other gluing occurs) it intersects exactly \(2\) times. These correspond to the values \(n=3\) and \(d=2\) we chose for the slope.

When we glue the edges together the horizontal edges become the equatorial circle on the torus while the vertical edges become a meridional circle.
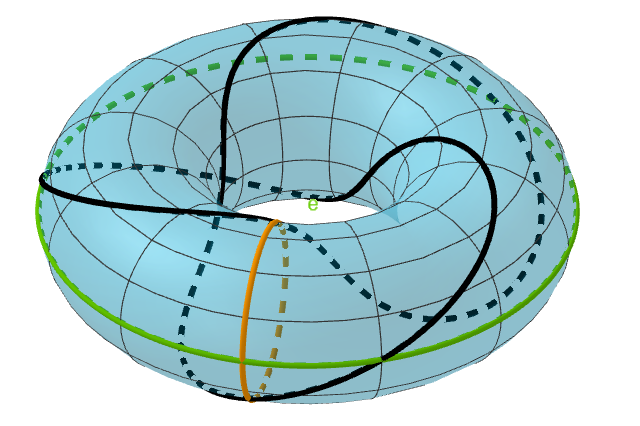
Notice that our intersections along the horizontal edge, because of the gluing, have become intersections of the knot with the equator. Similarly, intersections with the vertical edge became intersections of the knot with a meridian. Since the equator goes around the central hole these intersections tell us information about how many times the knot winds around the center. Since the meridian goes up and down, intersections with it tell us how many times the knot goes up and down.
The following table summarizes this information for a slope of \(3/2\):
| Slope: \(3/2\) | Information on identification diagram | Information on glued torus |
| \(3\) | Intersections with horizontal edge | Number of times knot winds around center |
| \(2\) | Intersections with vertical edge | Number of times knot goes up and down |
Question: In general, for a slope \(n/d\) what do the numbers \(n\) and \(d\) tell us?
Thinking Mathematically
Mathematicians often search for multiple ways to represent the same object in order to gain new insight. Typically one representation will emphasize a certain property whereas a different representation will emphasize another. In our case, we have two ways of representing curves on a torus -- either as lines on the identification diagram or as curves on the glued torus. While the former encodes all the geometric information of the curve (by looking at intersections with the edges, or the slope) it is difficult to visualize the curve. On the other hand, the latter makes it easy to visualize the curve but more difficult to compute the same geometric information.
Having multiple representations also serves another purpose. Let's say we had two ways to represent some phenomenon in 3D. One of the representations may easily generalize to higher dimensions but the other might not. If we only had one, it would be more difficult to describe the same higher dimensional phenomenon. For example, we can visualize the torus in 3D easily, but the identification diagram (surprisingly enough) gives a torus in 4D! If you notice, when we glue the edges of the identification diagram together we distort distances on it -- you necessarily have to stretch it out and bend it in order to connect the two ends of the cylinder together. What we're doing is taking the torus in 4D space and distorting it in such a way that we can actually view it in 3D space.
Quiz Questions
Solutions
Question 1
Wraps around the central hole five times, goes up and down three times.
Teaching Tips
Students do not need to determine the slope to answer this problem -- doing so may prove challenging. Instead remind students that they only need to count intersection points with the horizontal and vertical edges. There are five points of intersection along the horizontal edge (which becomes the equator), so the knot wraps around the central hole five times. There are three points of intersection along the vertical edge (which becomes a meridian), so the knot goes up and down three times.
Question 2
Slope: \(2/3\). Identification diagram:
Teaching Tips
This question is essentially the reverse of Question 1. Students need to count intersection points of the curve with the equator and meridian. Keep in mind that dashed lines are on the back side of the torus. So, a solid line "intersecting" with a dashed line is not a true intersection, it's simply due to the perspective. There are two intersections of the knot with the equator -- one is in the front left and the other in the back right. There are three intersections of the knot with the meridian -- two in the front right (one on top of the torus, the other below) and a third along the inner circle.
Since intersections with the equator give intersections along the horizontal, we need two equally spaced points, and the slope has numerator \(n=2\). Similarly three intersections with the meridian gives three equally spaced points along the vertical, and the slope has denominator \(d=3\). To draw the curve on the identification diagram, simply connect the points. Start with the bottom left point and go across to the middle of three points on the right vertical. If we connected to the lowest of the three we'd get a curve with slope \(1/3\). On the other hand if we connected to the top of the three (i.e., at the top right corner) we'd get a curve with slope \(3/3\). So, in between the two gives the correct slope.
Question 3
There are two closed curves. This is a link rather than a knot.
Bonus
The curve wraps around the other hole \(n\) many times.
Question 1
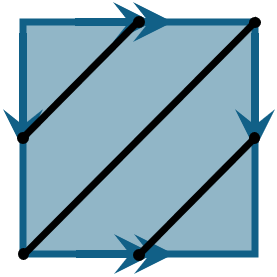
Below is an identification diagram for a torus with a closed curve drawn on it. Assume the single-arrow sides form a meridian and the double-arrow sides form the equator. How many times does the curve wind around the central hole? How many times does the curve go up and down?
Question 2
Below is a torus knot with a meridian and equator (black, orange, green respectively). Draw the curve on an identification diagram for the torus and write its slope.
Question 3
Below is an identification diagram of the torus. Is there a closed curve? If so, how many? Does it form a knot on the torus or a link?
Bonus
In the lesson we discovered that the denominator \(d\) of a curve with rational slope on a torus will wind around the central hole \(d\) many times. There is another hole in the torus -- when forming the torus, you first create a cylinder whose interior is a hole. Can you relate the number \(n\) to this hole on the torus?
Homework Questions
Solutions
Question 1
As \(T\) increases you trace out more and more of the torus. Thick bands begin to appear, but if you zoom in there are gaps.
Question 2
As \(T\) approaches infinity practically all of the torus gets traced out, but never all of it.
Teaching Tips
Again, this is an explorative problem, so answers may vary. It may be helpful to present some guiding questions -- for example, do you think the curve will ever close on itself (and form a knot)? Students might say that all of the torus gets traced. Have them zoom in a lot for large \(T\), and they should see that within the "bands" there are gaps.
In the lesson, all of the slopes were rational since they were expressed as a ratio of integers \(n\) and \(d\). This question explores what happens when the slope is irrational. Open Part 2 of the interactive torus knot generator, where one such curve is depicted. The slider \(T\) is for time -- as \(T\) increases, the curve gets traced out. Physically, this shows how much of the curve you've drawn with your pencil after some amount of time \(T\) has elapsed.
Test four to five different values of \(T\), then answer the following questions.
Question 1
What happens to the curve as \(T\) increases?
Question 2
What do you think will happen if the curve gets traced out forever (\(T\) continues to get larger and larger)?