- Author:
- Amanda Hager
- Subject:
- Mathematics
- Material Type:
- Lesson
- Level:
- Academic Lower Division
- Provider:
- University of Texas at Austin
- Tags:
- License:
- Creative Commons Attribution
- Language:
- English
- Media Formats:
- Text/HTML, Video
Correspondence Between Naturals and Rationals - Editable
2.5 Correspondences between infinite sets

Overview
| TCCNS Course | MATH 1332: Contemporary Mathematics |
| UT Austin Course | M 302: Introduction to Mathematics |
Introduction
Suggested Resources and Preparation
Materials and Technology
For the instructor: A worksheet to allow the students to generate their own curve through the rationals may be useful.
Prerequisite Assumptions
Students should know the definitions of the set of natural numbers, integers, and rational numbers.
Overview and Student Objectives
Lesson Length
75-100 minutes (1.5-2 fifty minute class meetings)
Lesson Objectives
Students will understand that:
- In order to prove that two infinite sets have the same cardinality, it is insufficient to say that both sets are infinite. We must give a one-to-one correspondence.
- There are multiple ways to write or represent a one-to-one correspondence: tables, curves, formulas, words.
Students will be able to:
- Visually depict an infinite set using ellipses.
- Visually represent a one-to-one correspondence between an infinite set.
- Use a visual representation of a one-to-one correspondence to generate a correspondence table between two infinite sets.
Correspondences between infinite sets
In this lesson, you learn two hard abstract proofs involving infinite sets.
Review: set notation and sets of numbers
To get started, you'll need to be able to write sets of numbers using set notation. The rules:
- We use curly braces { and } to denote sets (as opposed to brackets [ and ] which are used for intervals and parentheses which are used for intervals and points).
- Numbers in a set are always separated by commas.
- If a set is infinite, we list a minimum of three numbers in the list (but be sure to list enough that the pattern is obvious) and end with another comma and an ellipsis ...
- The numbers in a set do not have to be in any particular order. For example, \(\{1, 2, 3\}\) and \(\{1, 3, 2\}\) both represent the exact same set.
You'll also need to be familiar with the following four infinitely large sets of numbers. The symbols are in a font called "blackboard bold" and, while not strictly necessary for being successful in this course, are a universal and handy abbreviation.
| Set | Symbol | Definition |
|---|---|---|
| Natural numbers | \(\mathbb{N}\) | \(\{1, 2, 3, 4, 5, 6, \dots\}\) (some books include 0 but we will not) |
| Integers | \(\mathbb{Z}\) | \(\{\dots,-4, -3, -2, -1, 0, 1, 2, 3, 4, \dots\}\) |
| Rational numbers | \(\mathbb{Q}\) | \(\left\{\frac{a}{b}:a,b\mbox{ are integers, } b\neq0\right\}\) |
| Real numbers | \(\mathbb{R}\) | Any decimal number OR any location on a real number line |
Notice that every natural number is also an integer, every integer is also a rational number, and every rational number is also a real number. We could draw a Venn diagram for these relationships:
Integers vs. Naturals
Claim: The set of integers and the set of natural numbers have the same cardinality.
Proof: The first step is understanding this is an usual way to write down every integer in the world, but it is correct:
\(\{0,1,−1,2,−2,3,−3,4,−4,5,−5,\dots\} \)
Every integer is represented there. Using this, we can make a nice two-row table matching every natural number with every integer:
| Natural | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | ... |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Integer | 0 | 1 | -1 | 2 | -2 | 3 | -3 | 4 | -4 | 5 | -5 | ... |
Notice how some numbers show up in both rows, like 1, 2, 3, 4, etc. This is okay, in fact it's necessary. 3 is a natural number and it is also an integer.
What exactly counts as proof?
The table is the proof. That table is the bare minimum you need to show to prove these two sets have the same cardinality.
To make it more complete, you would add a sentence along the lines of "I will show a one-to-one correspondence between the two sets by displaying each element of both sets" or "The table below shows a one-to-one correspondence since each element of both sets is present in the table."
Video: Examples showing infinite sets that have the same cardinality
Rationals vs. Naturals
Claim: The set of rational numbers and the set of natural numbers have the same cardinality.
Proof: Once again, we show a two-row table that matches every natural with every rational, no leftovers, no repeats. The video explains how we build that table.
Video: Example: the natural numbers and rational numbers have the same cardinality
Quiz Questions
| Question | Answer |
| 1 | 3 |
| 2-1 | 5 |
| 2-2 | 1 |
| 2-3 | 2 |
| 2-4 | 7 |
| 3 | 1, 3, 50 |
| 4 | -2, 0, 1, 3, 50 |
| 5 | \(5, 0, \frac{17}{6}, -2.6\) |
Question 1
If I write the natural numbers like this:
\(\{1, 2, 3, 4, 5, 6, 7, 8, \dots\}\)
Which set represents a correct way to pair the integers with the natural numbers to demonstrate that the two sets have the same cardinality?
- \(\{1, -1, 2, -2, 3, -3, 4, -4, \dots\}\)
- \(\{\dots,-4,-3,-2,-1,0,1,2,3,4,\dots\}\)
- \(\{0,1,-1,2,-2,3,-3,4,-4,\dots\}\)
- \(\{0,1,2,3,4,\dots,-1,-2,-3,-4,\dots\}\)
Question 2
Match each of these sets with their expression in set notation:
Set Descriptions
- The set of all odd natural numbers
- The set of all odd natural numbers less than 10
- The set of all negative integers
- The set of all integer multiples of 6
Sets
- \(\{1, 3, 5, 7, 9\}\)
- \(\{-1, -2, -3, -4, -5, -6,\dots\}\)
- \(\{6, 12, 18, 24, 30, \dots\}\)
- \(\{1, 2, 3, 4, 5, 6, 7, 8, 9\}\)
- \(\{1, 3, 5, 7, 9,\dots\}\)
- \(\{1, 2, 3, 4 ,5, 6, 7, 8, 9,\dots\}\)
- \(\{\dots,-24,-18, -12, -6, 0, 6, 12, 18, 24,\dots\}\)
Question 3
Which of the following numbers are natural numbers? Select all that apply.
50, 0, -2, 1, 3, 2.5
Question 4
Which of the following numbers are integers? Select all that apply.
-2, 0, 3, 2.5, 50, 1
Question 5
Which of the following numbers are rational numbers? Select all that apply.
\(5, 0, 1.2345678910111213..., \frac{17}{6}, -2.6\)
Homework Questions
Question 2.5.1
- {1, 8, 27, 64, 125, ...}
- {1, 2, 3, 4, 5, 6}
- {-3, -1, 1, 3, 5}
- {-6,6}
Question 2.5.2
Preferred solution is a visual arrangement showing an even matching of elements of one set to elements of the other. 1 goes to 2, 2 goes to 4, 3 goes to 6, etc. Also can use formulas or functions, like "pair each natural number with a number that is twice as big."
Question 2.5.3
Best thing to do is match the numbers visually, again. 1 goes to 4, 2 goes to 9, 3 goes to 16, etc.
Question 2.5.4
Move everybody in the hotel up one room. Then all those people still get a room, and one room is opened up for the new person.
Question 2.5.5
Move everybody in the hotel up four rooms. Then all those people still get a room, and four rooms are opened up for the new people.
Question 2.5.6
Move everybody in the hotel to a room that is equal to twice their current room number. They all move into even-numbered rooms, and all the odd-numbered rooms are opened up for the new people.
Question 2.5.7
You can draw out the piles of tennis balls and then label each individual ball with a natural number to show the correspondence. So the first pile has ball #1, the second pile has balls #2, 3, the third pile has numbers #4, 5, 6. If you do this, you could conceivably draw a two-column table with little literal diagrams of tennis balls in one column, but I'm not sure what that adds.
Question 2.5.8
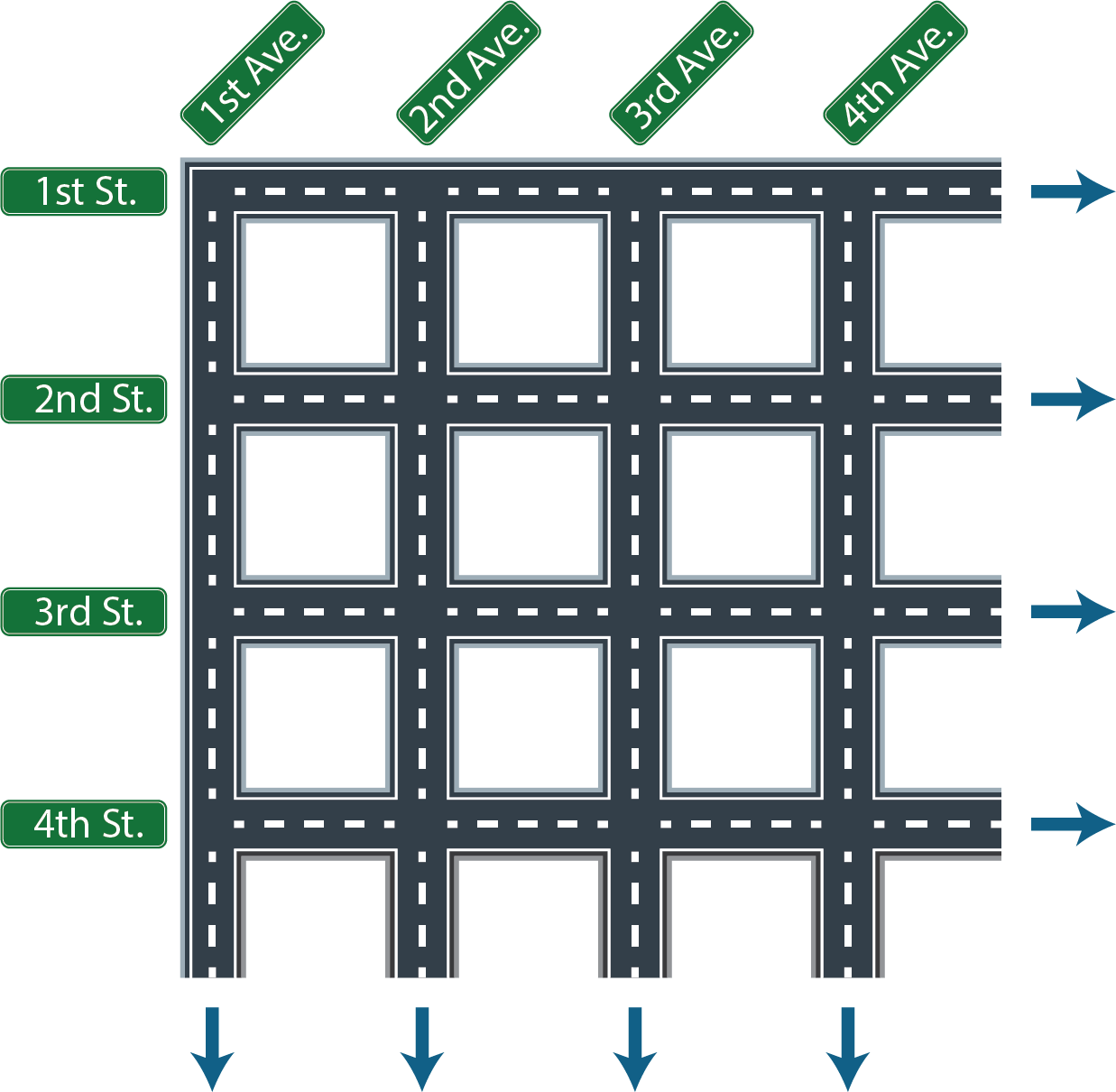
If you draw out the city grid and draw any kind of shape that goes through each and every intersection, you can use that grid like the "rationals spiral" to create a 1-1 correspondence. Im a fan of having 1st St and 1st Ave. (shorthand (1,1)) in the upper left, and then using this kind of scheme: (1,1) (2,1) (1,2) (3,1) (2,2) (1,3) (4,1) (3,2) (2,3) (1,4), ...
Question 2.5.9
If you arrange the streets and avenues in the style of Question 8, the grid of intersections looks precisely like the grid of fractions from the lesson. We can use a spiral shape through the intersections to be sure we are going through them all and listing them in a proper order.
Question 2.5.10
You are able to divide the time interval in half infinitely many times. If you always take the lowest numbered ball in the barrel, the barrel is empty after the full 60 second is over. The reason is that you can calculate the exact time that each individual ball goes in and comes out of the barrel without exception. Ball 2 goes in the barrel at t=30 and comes out at t=45. Ball 4 goes in the barrel at t=30 and comes out at t=56.25. Optional: Ball n comes out of the barrel at t=60(1-1/2^n).
Question 2.5.1
We can write the set of all natural numbers using set notation as \(\{1, 2, 3, 4,\dots\}\). Use set notation to express each of these sets:
- The set of all cubes of natural numbers
- The set of all natural numbers that are less than 7.
- The set of all even integers that are greater than -5 and less than 9.
- The set of all solutions of the equation \(x^2=36\).
Question 2.5.2
If we write \(\mathbb{N}\) to denote the set of all natural numbers, then the set of all even natural numbers could be written as \(2\mathbb{N}=\{2,4,6,8,10,\dots\}\). Show that \(\mathbb{N}\) and \(2\mathbb{N}\) have the same cardinality.
Question 2.5.3
Let \(A\) represent the set of all perfect squares of natural numbers that are higher than 1. This means that \(A=\{4,9,16,25,36,49,\dots\}\). Show that \(A\) and \(\mathbb{N}\) have the same cardinality.
Question 2.5.4
There is a magical hotel, called Hilbert's Hotel, that has as many rooms as natural numbers. Suppose one night a guest shows up and asks for a room. The problem is the hotel is completely full. There is one guest in every single room of the infinite hotel. But the guest is sad and tired, and the manager is sympathetic. How can the manager fit the new guest plus all of the other guests in the same set of rooms? Hint: no room-sharing. But you can make people move if you want.
Question 2.5.5
Now suppose that four new guests show up at Hilbert's Hotel, which is completely full with one guest in every room. How can you free up four rooms to fit the four new people?
Question 2.5.6
Finally, suppose that an infinitely long tour bus shows up, and infinitely many new guests show up, one for each natural number. Can the manager give each of these new people a room in the Hotel and still have rooms to give the old guests?
Question 2.5.7
You have an infinite number of tennis balls separated into piles. The first pile has one ball, the second pile has two balls, the third pile has three balls, and so on. This means that the nth pile has n tennis balls in it.
- Draw the piles of tennis balls.
- Create a single line that goes through every tennis ball in every pile.
- Use these drawings to prove that the overall set of tennis balls has the same cardinality as the set of natural numbers.
Question 2.5.8
Imagine an infinitely big city, with infinitely many avenues running north-south and infinitely many streets. There is an avenue for every natural number (1st Ave., 2nd Ave., 3rd Ave., etc.) and a street for every natural number (1st St., 2nd St., 3rd St., etc.). Prove that the set of intersections has the same cardinality as the set of natural numbers.
Question 2.5.9
Imagine an infinitely big city, with infinitely many avenues running north-south and infinitely many streets. There is an avenue for every integer (-2nd Ave., -1st Ave., 0th Ave., 1st Ave., etc.) and a street for every integer. Prove that the set of intersections has the same cardinality as the set of natural numbers.
Question 2.5.10
We have an infinite set of ping pong balls, a magically huge barrel, and a stopwatch set for 60 seconds. We start the countdown. When the time gets to 30 seconds we put ten ping pong balls into the barrel and then take one out. When the timer gets to 45 seconds (so half the remaining time is gone) we put one hundred balls into the barrel and then take one out. When half the remaining time is gone (52.5 seconds) we put one thousand balls into the barrel and then take one out. How many times are we able to divide the time in half and repeat this process? How many ping pong balls are left after the full sixty seconds is over?
Hint: There are multiple correct answers to this question depending on which ball you take out. I advise writing down some description of which balls are going in and which are coming out with each iteration.
Reflection/Application
Background
We learn to count when we are very young, and most of us don't stop and think about what a sophisticated skill that is. When we go all the way back and think about what it means to count, it leads to some surprising insights about fancier things like infinite sets.
Most things in our lives are more complicated than they seem or are more complicated that we really need to understand on a day-to-day basis. In almost every case, we can more effectively engage the world around us when we understand its complexity as much as possible.
Assignment
Think of another concept, issue, or skill that impacts your life that is more complicated than it seems. Write at least 200 words answering these questions:
- What makes this concept/issue/skill complicated?
- Why is it that you don't need to think about how complicated this concept/issue/skill really is on a day-to-day basis?
- What would it take to develop a more sophisticated understanding of the concept/issue/skill?
- Do you believe that a more sophisticated understanding of the concept/issue/skill would impact your life? Why or why not?