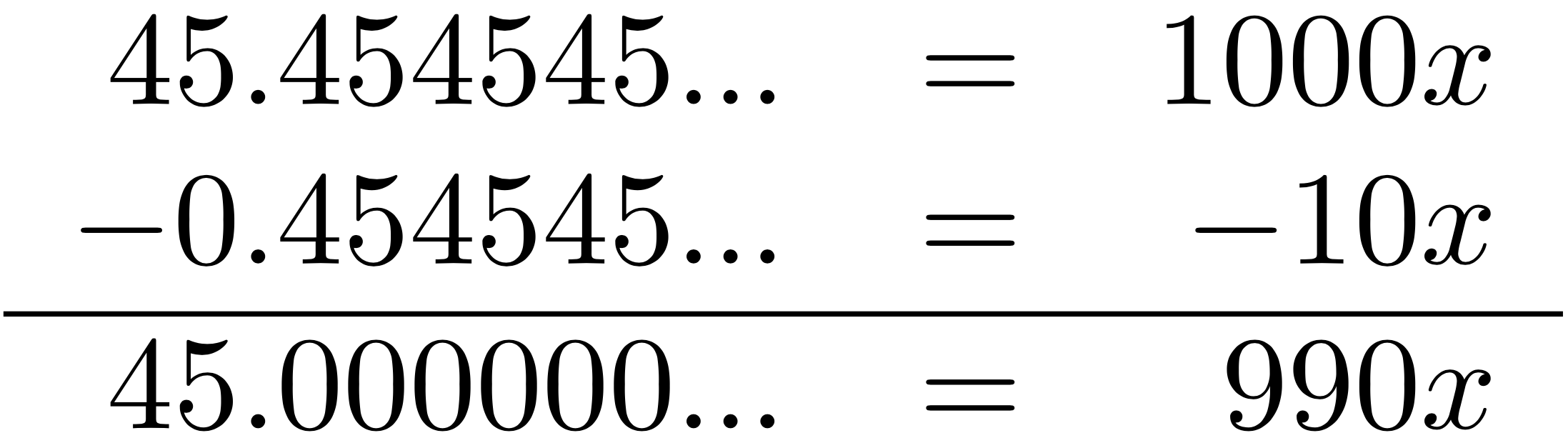2.3 Real numbers

Overview
| TCCNS Course | MATH 1332: Contemporary Mathematics |
| UT Austin Course | M 302: Introduction to Mathematics |
Introduction
Suggested Resources and Preparation
Materials and Technology
For the instructor: method for displaying or sharing video content.
For the student: grid paper may assist with lining up equations when converting decimals to fractions.
Prerequisite Assumptions
Students should be able to divide integers using long division.
Students should be able to manipulate linear equations using appropriate techniques.
Overview and Student Objectives
Lesson Length
50 minutes
Lesson Objectives
Students will understand that:
- By looking at or understanding the decimal expansion of a real number, we can tell whether the number is rational or irrational.
- The real numbers are well-ordered, and we can always put them in order using dictionary ordering.
Students will be able to:
- Order real numbers from least to greatest using their decimal expansions.
- Convert terminating decimals into fractions of integers.
- Convert real numbers with infinite repeating decimal expansions into fractions of integers.
Real numbers
Real Numbers
The punchline up front: there's this cool math test where you can look at any decimal number and tell right away if the number is going to be rational or irrational. We're going to use the test and we're going to prove the test works. Buckle up!
Background: what are real numbers, and how do we order them?
Terms
- A real number is any location on an infinitely long number line, known as the real number line.
- A rational number is a number that can be written as a fraction of integers a/b, where a and b are integers and b is not 0.
- An irrational number is a number that cannot be written as a fraction of integers a/b, where a and b are integers and b is not 0.
The real numbers can be thought of as points on a line because they are ordered. This means that if you call out two different points on the line, one will always be to the right and one will always be to the left. Similarly, if you call out two different real numbers, one will always be greater and one will always be lesser.
Side note, this is not an obvious thing! A lot of us have learned some basic math around matrices. Matrices are not ordered. Neither of these is "greater" than the other:
We compare numbers and decide which one is greater by using dictionary ordering. Read left to right, and go until you see digits that don't match. The higher digit corresponds with the greater number.
Examples
Q: Which comes first in the dictionary: cat or cob?
A: The first letters match. The second letters don't. a comes before o, so cat comes before cob. Notice that nobody cares that b comes before t.
Q: Which number is least: 1.5469 or 1.5380?
A: In this case the 1's and 5's match. The hundredths places are the first time the digits are different, and 3 is less than 4. Therefore, 1.5380 < 1.5469. Notice that nobody cares about the other decimal places.
Video: What are real numbers and how do we compare them?
Main Theorem
If a real number has a terminating decimal expansion or an infinite repeating decimal expansion, then it is a rational number.
If a real number has an infinite decimal expansion that never repeats, then it is an irrational number.
Proof Part 1: Turning (some) decimals into fractions
Finite decimal expansions
The trick for converting decimals with finitely many decimal places into fractions starts with understanding a trick for multiplying and dividing by 10. You get to just move the decimal point! Move it right if you are multiplying by 10's, and move left if you are dividing. You move the point one time for every power of 10. For example:
\(1.45×10=14.5\)
\(1.45÷10=0.145\)
\(1.45×1000=1450 \)
Second, you need to remember that you can alter fractions as long as you do the same thing to the numerator and denominator. So you multiply top and bottom by powers of 10 until you have a fraction of integers! For example:
\(1.45=\frac{1.45}{1}=\frac{145}{100}\)
\(0.8934=\frac{0.8934}{1}=\frac{8934}{10000}\)
\(−35.18=\frac{−35.18}{1}=\frac{−3518}{100}\)
Notice that we aren't reducing anything. Nobody cares about that right now. All that matters is "integer over integer." The fact that we can always do this is proof that all decimals with finite decimals expansions count as rational numbers.
Infinite repeating decimal expansions
We can also convert any infinite repeating decimal expansion into a fraction of integers. It just takes a little more work.
- Give your number a variable name. For example, write \(0.0454545...=x\).
- Multiply or divide by 10 until the decimal point is at the beginning of the "repeating part." For example, write \(0.454545...=10x\).
- Then multiply both sides by 10 until one copy of the repeating block is to the left of the decimal point and all the others are on the right. For example, \(45.454545...=1000x\).
- Subtract the smaller equation from the bigger equation. In this case, you would write:
The whole point is to get every decimal place to cancel out. If that doesn't happen, you made a mistake. - Solve the equation for x. In this case, you get \(x=\frac{45}{990}\). Do not reduce.
Video: Converting decimals into fractions
Proof Part 2: Turning fractions into decimals
Before studying this part, you may wish to review on long division of numbers, especially if your prior math classes were outside of the U.S. Khan Academy has a nice series of tutorials on it.
Let's start with a fraction of integers, like \(\frac{37}{7}\). When we express this number as a decimal, what kind of decimal do we get? Answer: you get an infinite repeating decimal expansion, and you know that the repeating block of digits can't be longer than 7 digits long. Here is a longer explanation:
Video: How do we know that rationals turn into repeating decimals?
Examples
Finite decimal expansions:
- \(\frac{38}{4}=9.5\)
- \(\frac{249}{2000}=.1245\)
- \(\frac{71}{32}=2.21875 \)
Infinite decimal expansions:
- \(\frac{2}{3}=.666...\) Denominator is 3, but repeating block of digits has only one digit.
- \(\frac{3}{11}=0.272727...\) Repeating block of digits is two digits long.
- \(\frac{99}{37}=2.675675675...\) Repeating block of digits is three digits long.
Summary
- If a decimal number has a finite or infinite repeating decimal expansion, then it is a rational number.
- Any fraction of integers can be converted into a decimal whose expansion will be finite or infinite repeating.
- Therefore, we know that the set of decimals with finite or infinite repeating expansions are exactly the rationals. That means that all the infinite non-repeating decimals expansions represent irrational numbers.
Quiz Questions
| Question | Answer |
|---|---|
| 1 | 1 |
| 2 | 1,4,5 |
| 3 | 2 |
| 4 | 1 |
| 5 | 2 |
| 6 | 3 |
Question 1
Is there a real number in between 0.1233333... and 0.124?
- Yes
- No
Question 2
Which of the following fractions works to prove that 0.125 is rational? Select all that apply.
- \(\frac{125}{1000}\)
- \(\frac{0.125}{1}\)
- \(\frac{125}{100}\)
- \(\frac{5}{40}\)
- \(\frac{1}{8}\)
Question 3
Is a number with an unending decimal expression is always, sometimes, or never irrational?
- Always
- Sometimes
- Never
Question 4
What is the number 0.49999... equal to?
- 0.5
- Slightly less than 0.5
- 4.9999.../10000...
- 4999.../9999...
Question 5
Using the technique from the module, which strategy works to compute the fraction representation of 0.123123123...?
- Move the decimal point over until you get to the end, and use 1,000,000,000... as a denominator.
- Set 0.123123123... equal to \(x\), then compute \(1000x\) minus \(x\) to find an equation that will help you find \(x\) as a fraction.
- Set 0.123123123... equal to \(x\), then compute \(10x\) minus \(x\) to find an equation that will help you find \(x\) as a fraction.
- Set 0.123123123... equal to \(x\), then compute \(123x\) minus \(x\) to find an equation that will help you find \(x\) as a fraction.
- Move the decimal point over nine times and then use 1,000,000,000 as a denominator.
Question 6
When we are finding the decimal expansion for 17/7, what is the largest number of digits that the repeating decimal expansion pattern could have?
- 17
- 3
- 6
- 7
- infinitely many
Homework Questions
Question 2.3.1
2.6=26/10, 9.81=981/100, 4.509899=4509899/1000000.
Question 2.3.2
3.44444...=31/9. Use 10x and x.
5.121212...=507/99. Use 100x and x.
4.1532532...=41491/9990. Use 10000x and 10x. Other solutions exist.
Question 2.3.3
Any number that starts with 4.610 or 4.611 and has a finite or infinite repeating decimal expansion will do. Except for 4.61 exactly, of course.
Question 2.3.4
Any decimal number that starts with 5.4 and has an infinite nonrepeating decimal expansion will do. For example, 5.412345678910111213... or 5.4010010001000010000010000001...
Question 2.3.5
4.353535...
0.2468101214161820...
0.2468101214161820
-2.910291029102...
-20
The first, third, fourth, and fifth numbers are rational. The first and fourth numbers are infinite repeating decimals expansions. The third and fifth numbers are terminating decimals. The second number is irrational because it has an infinitely long non-repeating decimal expansion.
Question 2.3.6
Mindset question. Responses will vary.
Question 2.3.1
Express these numbers as fractions of integers: 2.6, 9.81, 4.509899.
Question 2.3.2
Express these numbers as fractions of integers:
3.44444...
5.121212...
4.1532532532....
Question 2.3.3
Find a rational number that is between 4.61 and 4.612. Explain how you know your number is rational.
Question 2.3.4
Find an irrational number that is between 5.4 and 5.5. Explain how you know your number is irrational.
Question 2.3.5
Which of these numbers are rational and which are irrational?
4.353535...
0.2468101214161820...
0.2468101214161820
-2.910291029102...
-20
Question 2.3.6
Think of a question regarding real numbers, rational numbers, and/or irrational numbers that goes beyond what you were taught in this section. For example, you can extend one of the theorems, guess at whether something is always/sometimes/never true, or ask about a brand new property altogether.
You do not need to answer this question, just find a way to phrase the question so it is as clear as possible.