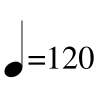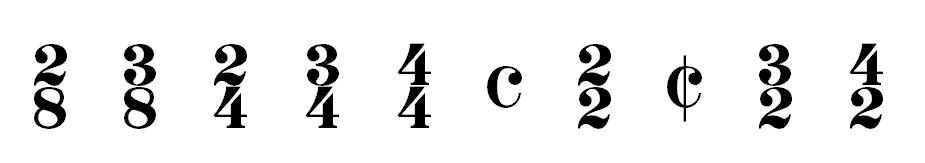- Author:
- Stephen Emmons
- Subject:
- Performing Arts
- Material Type:
- Textbook
- Level:
- Academic Lower Division
- Tags:
- License:
- Creative Commons Attribution Non-Commercial Share Alike
- Language:
- English
Education Standards
Lead Sheet Symbols and Roman Numerals exercises
Pitch, Scales, and Keys - exercises
Rhythm, Meter, and Beaming - exercises
Roman Numerals & Lead-Sheet Symbols
Triads and Seventh Chords exercises
A Survey of Music Theory for the College Classroom: Fundamentals

Overview
A Survey of Music Theory for the College Classroom is a concise, practical, and readable text and workbook for use in the freshman and sophomore music theory curriculum.
Introduction
A Survey of Music Theory for the College Classroom is a concise, practical, and readable text and workbook for use in the freshman and sophomore music theory curriculum. The text is divided into four parts which are linked by a table of contents, allowing for a seamless transition between them.
A Survey of Music Theory for the College Classroom: Fundamentals
A Survey of Music Theory for the College Classroom: Diatonic Harmony
A Survey of Music Theory for the College Classroom: Chromatic Harmony I
A Survey of Music Theory for the College Classroom: Chromatic Harmony II and 20th Century Music
Most chapters include PDFs of exercises and excerpts for analysis. I encourage the instructor to supplement the course materials through the analysis of lengthy excerpts or complete pieces of music, especially during the sophomore year. I also highly recommend the use of Rising Software’s Musition (theory) and Auralia (aural skills) software. The Musition and Auralia software package is robust, customizable, and can be used to reinforce most concepts covered in freshman and sophomore theory. I have also written a comprehensive set of exams as well as about 1100 objectives questions for use in Blackboard. Please email me at semmons@angelo.edu from a valid faculty email address if you would like to access these tests or Blackboard pools.
In addition to the extensive excerpts for analysis, the reader will note the prevalence given to part-writing, especially in the books Diatonic Harmony and Chromaticism I. In my experience, part-writing is the laboratory in which the student can learn many of the fundamentals of music theory. Additionally, I have found that students enjoy and even prize the time spent at the boards actively learning through part-writing and the completion of similar in class exercises.
The examples from the literature in the text and workbook were taken from the IMSLP that are public domain in the United States. I wrote all the part-writing and short examples in the text, all the exercises for the workbook, and a few pieces for analysis that demonstrate various techniques.
I dedicate this book to the late Dr. Edward Pearsall and the late Dr. Mary Jeanne van Appledorn. I studied Schenkerian analysis and 20th century theory with Ed during my doctorate at Texas Tech. Through these classes and as a member of my dissertation committee, he had a profound influence on my understanding of music and on my writing. Dr. Van was one of a kind. I studied composition and theory with her during my doctorate, and she was a master teacher of composition, the use of scales, and the music of Debussy. I have happy memories of sitting with her at the piano banging through my music or analyzing various 20th century works. She taught with great care and with humor. I shall always be in her debt.
Stephen D. Emmons, Ph.D.
Table of Contents
A Survey of Music Theory for the College Classroom: Fundamentals
- Pitch, Scales, and Keys
- Intervals
- Rhythm, Meter, and Beaming
- Triads and Seventh Chords
- Lead-Sheet Symbols and Roman Numerals
A Survey of Music Theory for the College Classroom: Diatonic Harmony
- Harmonic Progression
- Texture, Voice Leading and Counterpoint
- Root Position Part-Writing
- First Inversion Triads
- Second Inversion Triads
- Cadences and Small-Scale Form
- Nonchord Tones
- Second and Fourth Species Counterpoint
- Dominant Seventh Chords
- Leading Tone Seventh Chords
- Nondominant Seventh Chords
A Survey of Music Theory for the College Classroom: Chromatic Harmony I
- Secondary Dominants
- Secondary Leading Tone Chords
- Modulation
- Binary and Ternary Form
- Borrowed and Neapolitan Chords
A Survey of Music Theory for the College Classroom: Chromatic Harmony II and 20th Century Music
Pitch, Scales, Keys
Pitch, Scales, and Keys - Blackboard pools
- Pitch, Scales, and Keys
- Leading Tones
Notation of Pitch
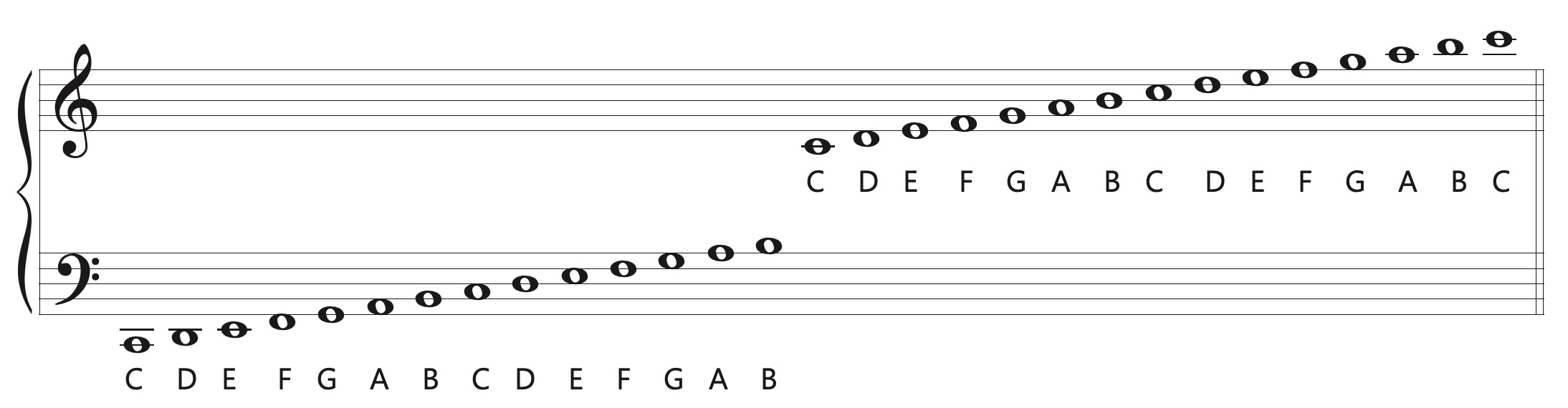
Pitch refers to how high or low a note sounds. Pitches are named after the first seven letters of the alphabet, also called the musical alphabet, and are notated on a staff. The treble clef is normally used for higher pitches, and the bass clef is normally used for lower pitches. The grand staff consists of two staves joined by a brace. Ledger lines are used to extend the range above and below the staff.
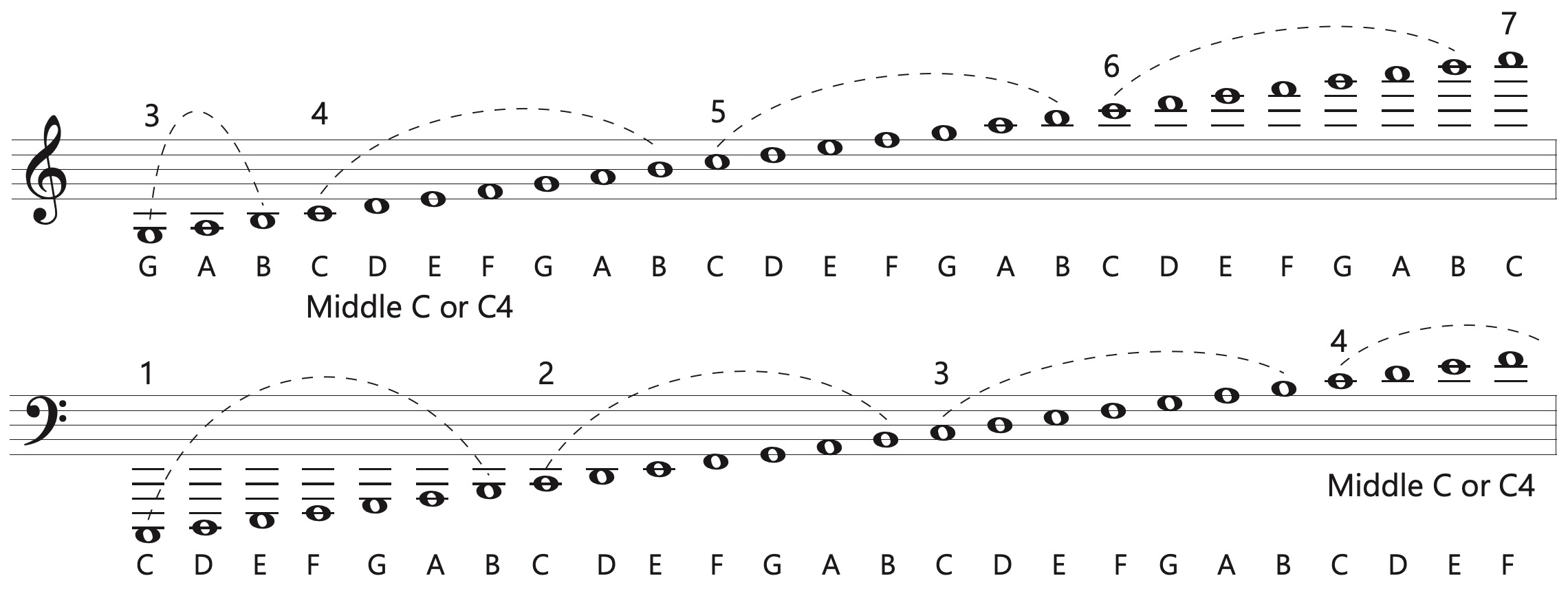
Octave register designations allow us to name a specific pitch. We say “C4” rather than just “C” when we want to identify middle C. A pitch class includes all the notes with the same name – for example pitch class C.
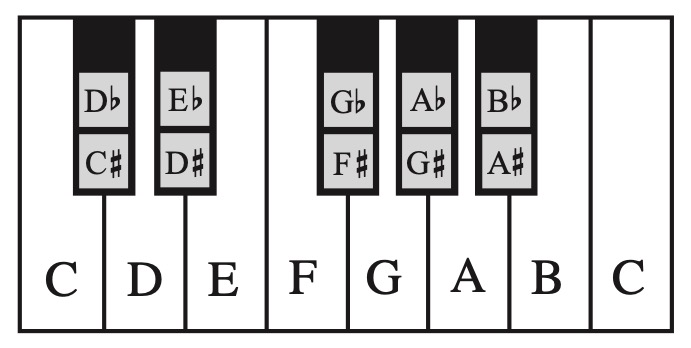
The concept can also be illustrated on the piano keyboard.
Tenor clef is commonly used by bass clef instruments when playing in their highest registers. Alto clef is used by the viola. This is the note C4 or middle C in the treble, alto, tenor, and bass clefs.
Major Scales
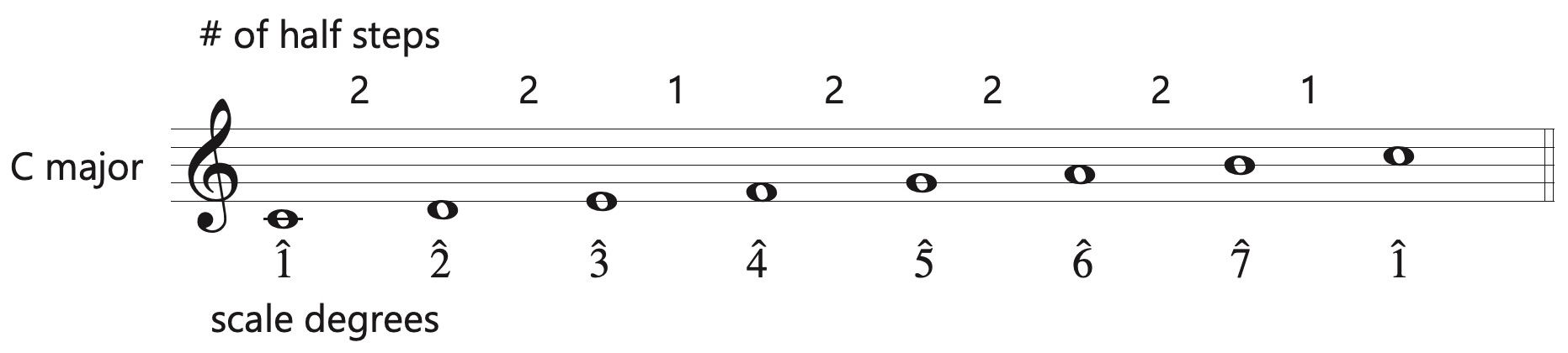
Scales are successions of pitches arranged in half steps and whole steps. Western music from about 1600-1900, which is called the Common Practice Period, primarily uses major and minor scales. Since much of the music we listen to and teach is from this period, we will begin by discussing the major and minor scales.
The half step or semitone is the smallest interval in tonal music. An interval is the distance between two notes. Any two piano keys that are next to one another are a half step apart. This pattern is most commonly a white key to a black key, but the white key notes E to F and B to C are also half-steps. A whole step or whole tone is simply two half steps.
The following are the scale degree names in major keys. A number with a caret (^) above it is a short way of writing scale degrees.
\(\hat{1}\) = Tonic
\(\hat{2}\) = Supertonic
\(\hat{3}\) = Mediant
\(\hat{4}\) = Subdominant
\(\hat{5}\) = Dominant
\(\hat{6}\) = Submediant
\(\hat{7}\) = Leading Tone
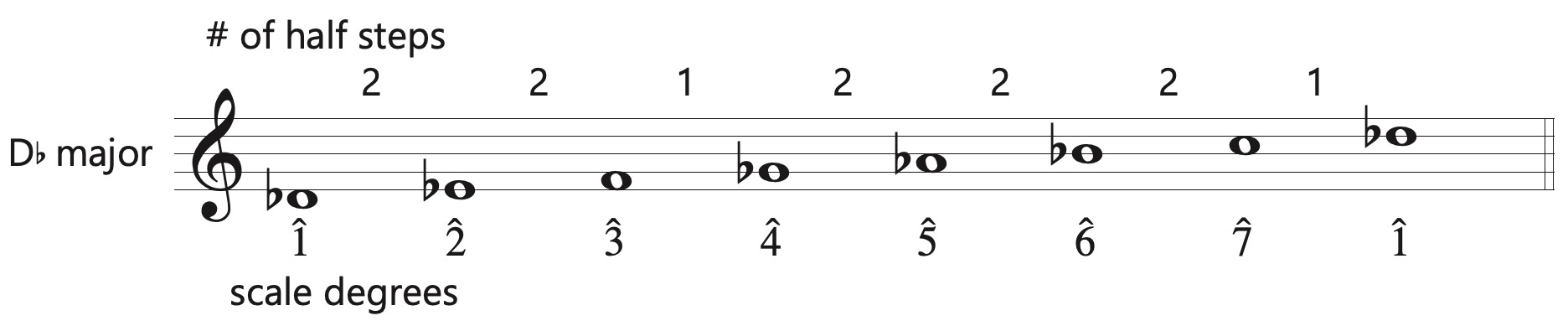
To construct major scales on other tonics we need to use accidentals.
♯ (sharp) – raises a white key pitch by a half step
♭ (flat) – lowers a white key pitch by a half step
♮ (natural) – cancels an accidental (refers to white keys on the piano)
x (double sharp) – raises a white key pitch by a whole step
♭♭ (double flat) – lowers a white key pitch by a whole step
Scales are always named for the tonic note. In this case it is D♭.
Key Signatures
Key signatures are derived from the accidentals required to make a scale on a given note and are named after the tonic of the scale. While it is important to understand and be able to apply the pattern of half steps and whole steps in creating major scales, it is also essential to memorize all the key signatures for the major and minor scales.
Flats and sharps appear in key signatures in a predictable manner. This order of flats and sharps is as follows:
Order of flats = B E A D G C F
Order of sharps = F C G D A E B
For example, if a key signature has two flats, they will be B♭ and E♭, and if a key signature has three sharps, they will be F♯, C♯, and G♯. In modern publications, key signatures appear in a certain way. Below is a graphic that shows how all key signatures should be written in the four most common clefs.
Enharmonic Equivalence
Some notes on the piano have two names, for example C♯ and D♭. This is called enharmonic equivalence. Enharmonic notes sound the same because they are the same pitch. Enharmonic notes can share black keys or white keys, such as the notes C♭ and B♮.
Minor Scales
There are three forms of the minor scale: natural minor, harmonic minor, and melodic minor. The natural minor scale uses only the accidentals found in that scale’s key signature, while both the harmonic and melodic minor scales use accidentals not found in the key signature. Melodic minor also includes a descending form of the scale in which the scale reverts to natural minor.
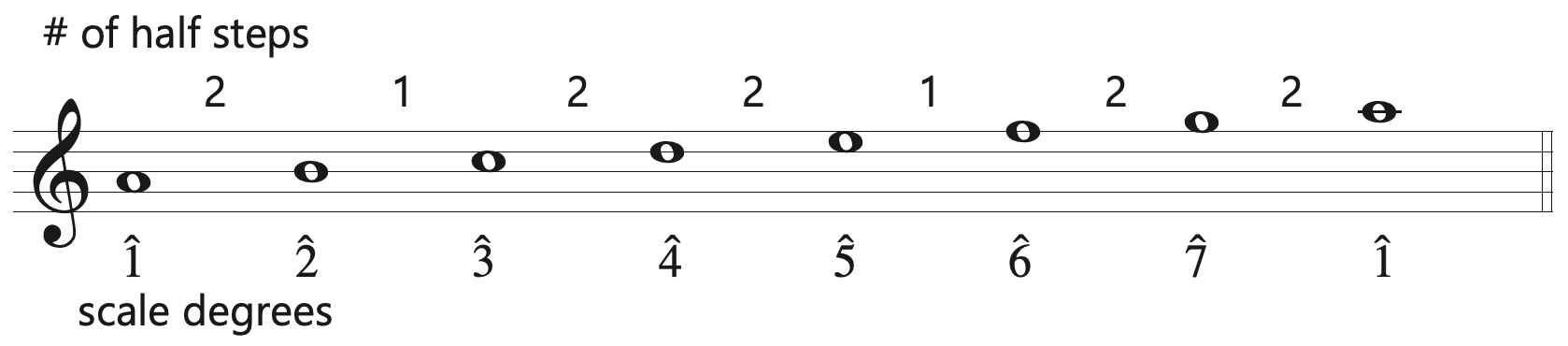
This is the a natural minor scale.
The names of the scale degrees are the same as they are for major scales with one exception. In natural minor, scale degree \(\hat{7}\) is a whole step below the tonic and is referred to as the “subtonic.” In harmonic and melodic minor, the seventh scale degree is a half-step below the tonic and is called the “leading tone” as it is in major.
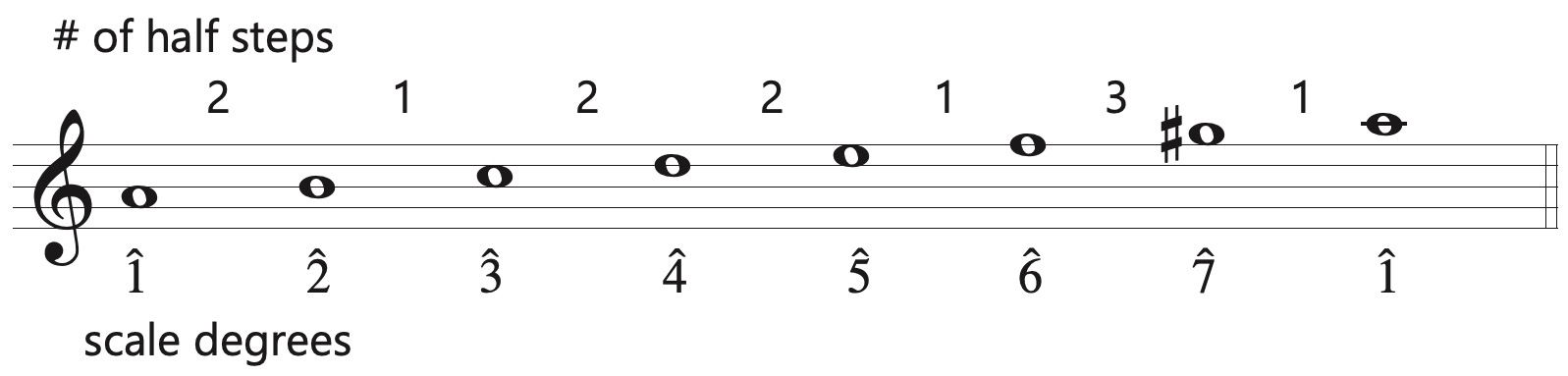
This is the a harmonic minor scale.
This is the a melodic minor scale.
Minor scales can be constructed by counting half-steps, by modifying the parallel major, or by using the concepts of relative major and minor keys. Parallel major and minor scales have the same tonic note but use different key signatures. Relative major and minor scales have different tonic notes but use the same key signature.
Parallel Major Method
Below is a C major scale. If the c natural minor scale is desired, then scale degrees \(\hat{3}\), \(\hat{6}\), and \(\hat{7}\) of the C major scale should be lowered by a half-step or semitone. If the c harmonic minor scale (ascending) is needed, then scale degrees \(\hat{3}\) and \(\hat{6}\) should be lowered by a single half-step, leaving scale degree \(\hat{7}\) untouched. If the melodic minor scale (ascending) is needed, then only scale degree \(\hat{3}\) should be lowered by a half-step. Remember that the descending version of the melodic minor reverts to natural minor.
Relative Key Method
The concept of relative major and minor keys can also be used to build minor scales. For example, if you want to construct a g natural minor scale, you need to know the key signature of its relative major. The tonic notes of relative major and minor keys are a m3 or three semitones apart. The third scale degree of a minor scale is the tonic of its relative major, and the sixth scale degree of a major scale is the tonic of its relative minor.
B♭ major’s key signature has two flats. The key signature of g minor has the same two flats.
If you want to construct the harmonic minor scale, raise scale degree \(\hat{7}\) by one semitone.
If you want to construct the melodic minor scale in ascending form, raise scale degrees \(\hat{6}\) and \(\hat{7}\) by one semitone.
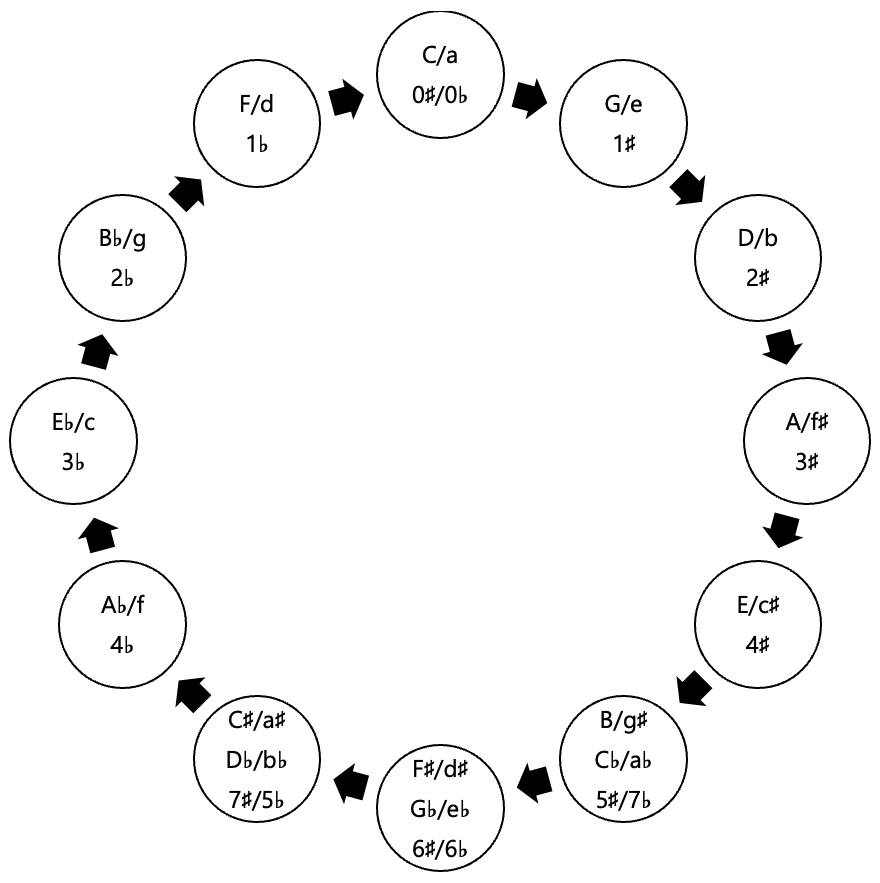
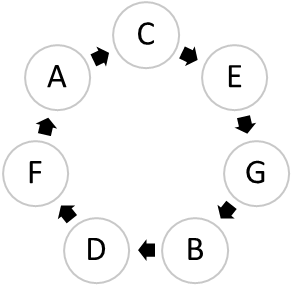
Circle of Fifths
The circle of fifths is a way of illustrating all the major and minor keys and the concept of relative keys. As you travel clockwise around the circle, each tonic is a P5 above the previous tonic. In other words, each key starts on the dominant scale degree of the previous key. As you travel counterclockwise around the circle, each tonic is a P5 below the previous tonic. Therefore, each key starts on the subdominant scale degree of the previous key. Note the enharmonic keys on the circle of fifths. The major keys are in upper case letters, and the relative minor of each major key is in lower case.
The Chromatic Scale
The last scale we will discuss in this chapter is the chromatic scale, which consists of only half steps. The ascending chromatic scale is usually written with sharps, while the descending chromatic scale is commonly written with flats.
Intervals
Intervals - Blackboard pools
- Intervals pool
- Interval Quantities
Intervals
An interval is the distance between two pitches. Intervals are harmonic when two pitches are played or sung at the same time and are melodic when two pitches are played or sung one after another in a melody. Intervals are simple when they are an octave or less in distance and are compound when they exceed an octave.
Numbers and Qualities
Intervals are identified by a number and a quality. The half step (semitone) is the smallest interval in tonal music. Any two piano keys that are next to one another are a half step apart. This pattern is most commonly a white key next to a black key, but the white key notes E to F and B to C are also half steps.
- Interval qualites include perfect (P), major (M), minor (m), augmented (+), and diminished (o).
- Generic intervals that can be perfect include the 1, 4, 5, and 8 (1 = unison and 8 = octave).
- Generic intervals that can be major or minor include the 2, 3, 6, and 7.
- Any interval can be augmented or diminished.
- Perfect intervals can be made larger or smaller by a half step.
° ↔ P ↔ + - Major and minor intervals can be made larger or smaller by a half step.
° ↔ m ↔ M ↔ +
Just as there are enharmonic spellings for notes, there are enharmonic intervals as well. The +6 sounds the same as a m7 but is spelled differently. An +6 above C is an A♯, while a m7 above C is a B♭. The A♯ and B♭ are enharmonic and are both 10 half steps (semitones) above C, but the C to A♯ is counted as a sixth and the C to B♭ as a seventh. Doubly augmented intervals can be created by expanding an augmented interval by one semitone, and doubly diminished intervals can be created by contracting a diminished interval by one semitone. Such intervals are rare in music, and we will not otherwise consider them in this text.
This is a list of commonly encountered intervals. This list is not exhaustive.
Interval Name | # of semitones |
P1 | 0 (unison) |
m2 | 1 |
M2 | 2 |
+2 | 3 |
m3 | 3 |
M3 | 4 |
P4 | 5 |
+4 | 6 (tritone) |
°5 | 6 (tritone) |
P5 | 7 |
m6 | 8 |
M6 | 9 |
+6 | 10 |
m7 | 10 |
M7 | 11 |
P8 | 12 (octave) |
Identification of Intervals
Major Scale Method
There are a few ways to identify intervals. One method is to use the intervals found between scale degrees in the major scale.
Step 1 Count the interval’s numerical name. Start on the bottom note and call it “1” and continue to the top note. Do not skip a note name. In the following example, D = 1, E = 2, F = 3, G = 4, A = 5, and B = 6. The numerical name for this interval is a 6th.
Step 2 Think of the bottom note as the tonic of a major scale. Is the note “B” the normal sixth scale degree in D major? Yes, it is, which makes this a M6.
White Key Method
Another method of determining and writing intervals is called the white key method. While this does require memorizing all the intervals between the white keys of the piano, it is a powerful tool and allows very quick identification and writing of intervals.
Below are the white key seconds. Five of them are major seconds and two are minor seconds.
Next are the white key thirds. Four of them are minor thirds and three are major thirds.
These are the white key fourths. All of them are perfect except for F-B.
While fourths invert to fifths (see Interval Inversion) and can therefore be easily calculated, the fifths are included here because of their utility in building chords.
These white key intervals can be expanded or contracted by a half-step. For example, E to G is a minor third apart. If we lower the E by a semitone, the E♭ to G is now a major third apart. If we apply the same accidental to any of these white key intervals, the interval quality stays the same. For example, the notes C♮ and E♮ are a major third apart. The notes C♭ and E♭ are also a major third apart, as are the notes C♯ and E♯.
Interval Inversion
Inversion of an interval occurs when the bottom pitch is placed above the top pitch or when the top pitch is placed below the bottom pitch. To find the inversion of an interval, subtract the number of the interval from 9. The number 9 is a constant value because the sum of an interval and its inversion will always add up to 9.
7ths invert to 2nds
6ths invert to 3rds
5ths invert to 4ths
Major intervals become minor
Minor intervals become major
Perfect intervals remain perfect
Diminished intervals become augmented
Augmented intervals become diminished
By using the concept of inversion, it is easy to calculate the sixths and sevenths using the white key method. The major second between the notes C and D, for example, inverts to a minor seventh between D and C. If we make that one semitone larger, we have a major seventh between D and C♯.
Writing an Interval Above a Given Note
Major Scale Method
You can use the major scale method or the white key method for writing intervals above a given note.
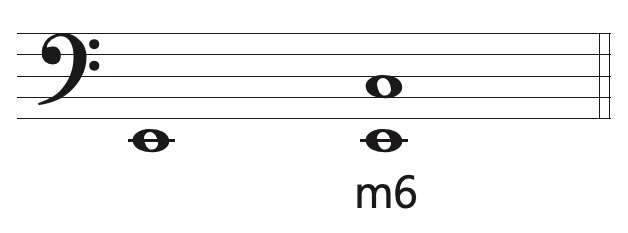
Example: Write a m6 above the given note E.
Step 1 Write the note a sixth above E, using E as 1. The note a sixth above E is C.
Step 2 Think in the key of the bottom note, which is E major. The note C♯ is the sixth scale degree in the key of E major and is therefore a M6 above C. The C♮ is a m6 above E.
Sometimes you will have to write an interval above a note that is the tonic of an unusual key, such as F♭.
Example: Write a P5 above F♭
Remove the flat so that you are now thinking in the key of F. The P5 above F is C. When you add the flat back to the F, you must also add a flat to the C to maintain the P5.
Writing an Interval Below a Given Note – Inversion Method
You can use the concept of inversion to write an interval below a given note. When using the inversion method, you first invert the interval and find this interval above the given note. After this note is found, you will then place it an octave lower thus putting the note below the given pitch.
Example: Write a P4 below the given note
Consonance and Dissonance
Intervals are categorized as consonant or dissonant based on their sound and harmonic stability. Consonant intervals are more stable and “sweet” in sound. Dissonant intervals are less stable and “harsher” in sound.
Consonant harmonic intervals include the following:
- Major and minor thirds and sixths (M3, m3, M6, m6)
- Perfect intervals except the P4 (P1, P5, P8)
Dissonant harmonic intervals include the following:
- Major and minor seconds and sevenths (M2, m2, M7, m7)
- Tritones – the o5 and +4
The perfect fourth (P4) is a special case. It is dissonant when it is the first interval above the lowest note (the "bass" note). This is true when it is part of a dyad, which is when two pitches are sounding together. It is also true when it is part of a triad, which is when three pitches sound together as a chord. It is consonant, however, when it is supported by a third below it.
Rhythm, Meter, Beaming
Rhythm, Meter, and Beaming - Blackboard pools
- Rhythm, Meter, and Beaming
Rhythm
Rhythm is the time element in music. It is one of the fundamental elements in music, along with melody, harmony, dynamics, texture, timbre, articulation, and register. Indeed, rhythm is often the most recognized facet in many pieces of music.
Basic Elements of Notation
Before we explore rhythm, we need to survey the basic building blocks of music notation. So far, we have only used whole notes when writing music. Stems, beams, flags, and dots allow us to access more complex rhythms. A flag shortens a note’s duration by half. Flags are combined into beams when two or more notes are grouped together.
Stem Direction
We will adhere to the following basic rules for stem directions.
- Single notes on or above the middle line of the staff – stem direction is down.
- Single notes below the middle line of the staff – stem direction is up.
- Two beamed notes unequal in distance from the middle line of the staff – stem direction is determined by the note farthest in distance from the middle line of the staff.
- Two beamed notes that are the same distance from the middle line of the staff – stem direction is down.
- Three or more beamed notes – stem direction is determined by the note the greatest distance from the middle line. If there is a tie for greatest distance, all stems are down.
Rhythmic Values
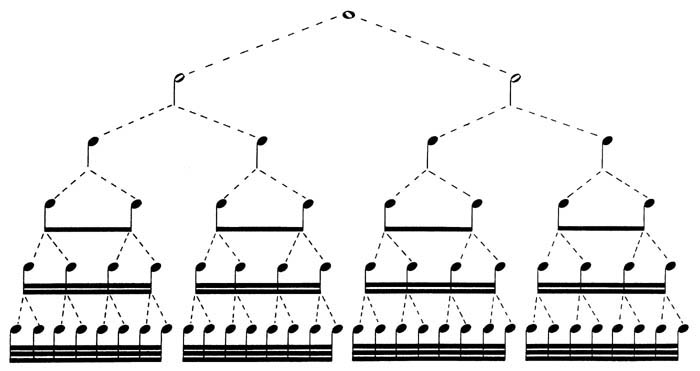
The notation of rhythm involves a basic set of symbols of sound and silence. The following “rhythm tree” shows note values from the whole note through the thirty-second note. Observe that undotted notes divide into two equal parts.
For every symbol of sound there is a corresponding symbol of silence. While it may seem counterintuitive, silence is just as important as sound in music.
Dots and Ties
Dots and ties can be used to create more flexibility in rhythmic values. A dot increases the duration of a note or rest by one-half its original length. An additional dot will add half the value of the original dot.
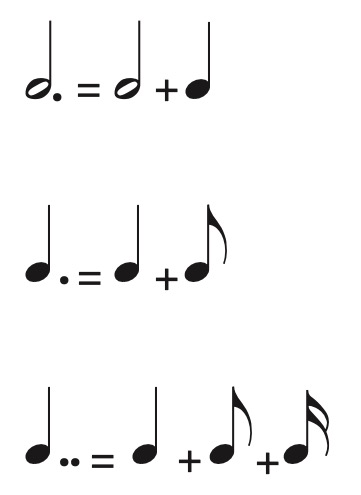
A tie connects two notes that are the same pitch. The tied notes are to be played as a single note with the rhythmic values added together. They can be used to connect pitches within a measure as well as over bar lines.

Meters, Division of the Beat, and Time Signatures
The beat is the pulse of the music. It is what we clap to, dance to, and march to. Tempo describes how fast the beats occur. It is described using words, usually in Italian, and by using metronome markings. Metronome or tempo markings show how many beats occur in a minute. The following metronome marking means that there are 120 quarter notes occurring every minute, or two a second.
Some beats are accented and are stronger than other beats. The first beat or downbeat in a measure is always strong. This naturally occurring accent on the downbeat in a measure is called a metric accent.
Meters
Meters are classified as duple, triple, and quadruple depending on the number of beats within each measure.
- Duple meters contain two beats in a strong / weak pattern.
- Triple meters contain three beats in a strong / weak / weak pattern.
- Quadruple meters contain four beats in a strong / weak / somewhat strong / weak pattern.
These patterns of strong and weak beats are the foundation of the conducting patterns that are used in bands, orchestras, and choirs. Below are the basic patterns for duple, triple, and quadruple meters.
Division of the Beat
Beats are classified as simple or compound depending on the division of the beat into two or three equal parts. Both simple and compound meters can be duple, triple, or quadruple.
- Beats that divide into 2 equal parts are called simple beats. The beat notes in simple meters are undotted values.
- Beats that divide into 3 equal parts are called compound beats. The beat notes in compound meters are dotted values.
Time Signatures
Time signatures show how many beats are in a measure and which note value gets a beat. Time signatures for simple beats have 2, 3, or 4 at the top. The top number shows the number of beats in a measure, while the bottom number shows the beat note value. Simple meters with 2 at the top are duple, those with 3 at the top are triple, and those with 4 are quadruple.
If the bottom number in a time signature is 4, the quarter note is the beat note. If the bottom number in a time signature is 8, the eighth note is the beat note. If the bottom number is 2, then the half note is the beat note.
Some common simple meters are:
Time signatures for compound beats have 6, 9, or 12 at the top. The top number shows the number of divisions in a measure, while the bottom number shows the division value. Dividing the top number by 3 will yield the number of beats in the measure. For example, 6 ÷ 3 = 2, which means that time signatures with 6 as the top number are duple meters. Also, 9 ÷ 3 = 3, which means that time signatures with 9 as the top number are triple meters. In addition, 12 ÷ 3 = 4, which means that time signatures with 12 as the top number are quadruple meters.
A compound time signature with a bottom number of 8 means that the division is an eighth note and that the beat is a dotted quarter. A compound time signature with a bottom number of 16 means that the division is a sixteenth note and that the beat is a dotted eighth. A compound time signature with 4 at the bottom means that the division is a quarter and that the beat is a dotted half.
Some common compound meters are:
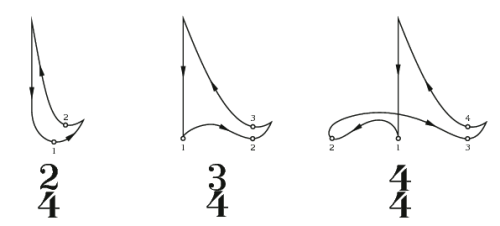
Beaming and the Notation of Rhythm
Beaming is the practice of grouping beats and subdivisions into easy to read and interpret visual packages. Beams connect two or more notes that are within the same beat in both compound and simple meters. Beams should help to clarify the natural metric accents that occur within a meter. As you can see from the next example, beamed rhythms are much easier to read than non-beamed rhythms.
Syncopation
Syncopated rhythms displace the regular metric accents within a meter. The following illustrates the standard way of notating a common syncopated rhythm.
Borrowed Divisions (Tuplets)
When writing music in a simple meter, composers can borrow the triple division of the beat from compound meters. These borrowed divisions are called triplets. Similarly, when writing music in a compound meter, composers can borrow the duple division of the beat from simple meters. These borrowed divisions are called duplets. It is also possible to create quadruplets, quintuplets, sextuplets, and septuplets. The illustrations below only touch upon the range of tuplets available.
Triads and Seventh Chords
Triads and Seventh Chords - Blackboard pools
- Triads and Seventh Chords
Chords
Chords are combinations of three or more pitch classes that are sounded together simultaneously or in an arpeggio. The chord types that we will learn about in this chapter are built of stacked major and minor thirds and are called triads and seventh chords. The four types of triads and the five most common seventh chords are extremely important in Western music. Each has a different structure and a unique sound. The structures of these chords should be memorized.
The charts below illustrate the seven possible spellings for triads and seventh chords using the natural notes of the musical alphabet. Accidentals (♯, ♭, ♮, x, ♭♭) can be added to these notes as needed. The root is the note upon which a triad or seventh chord is built.
Triads
R 3rd 5th
C E G
D F A
E G B
F A C
G B D
A C E
B D F
Seventh chords
R 3rd 5th 7th
C E G B
D F A C
E G B D
F A C E
G B D F
A C E G
B D F A
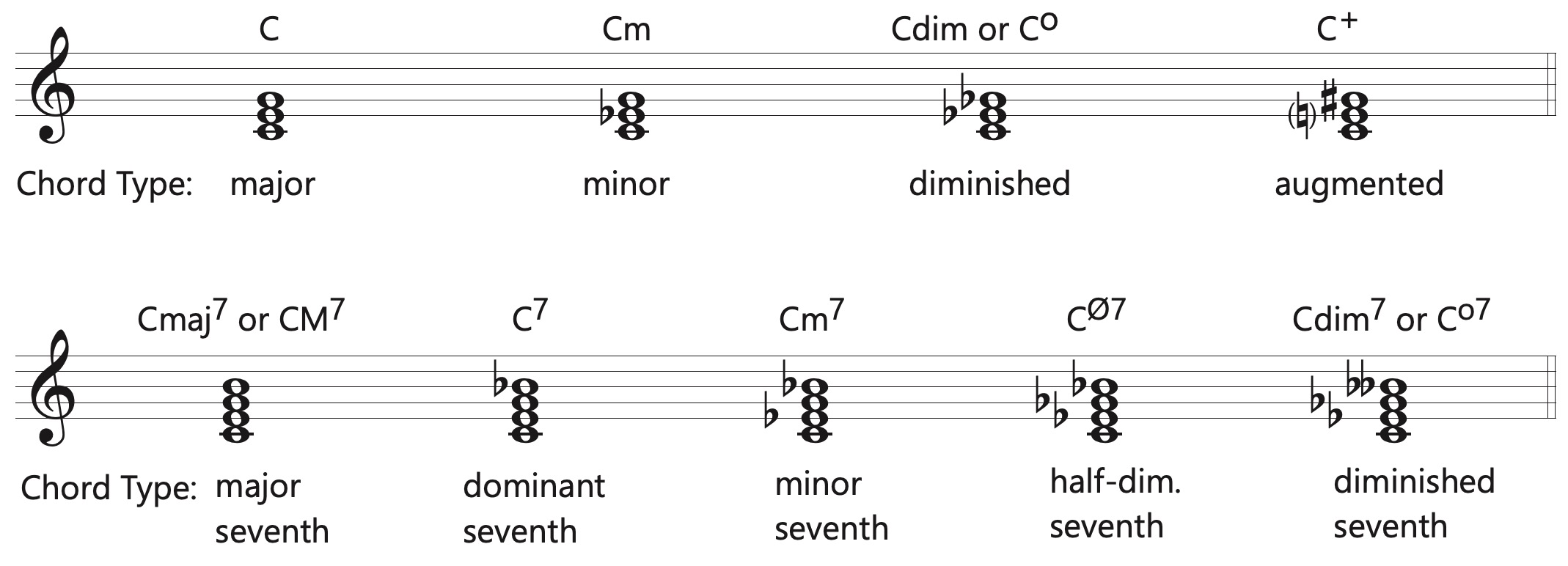
The Four Triads
The four types of triads are illustrated below. The bottom note in each case is the root of the chord.
- The major triad consists of a M3 and P5 above the root. This chord can also be understood as stacked thirds with a M3 above the root and a m3 above the third.
- The minor triad consists of a m3 and P5 above the root. This chord can also be understood as stacked thirds with a m3 above the root and a M3 above the third.
- The diminished triad consists of a m3 and o5 above the root. This chord can also be understood as stacked thirds with a m3 above the root and a m3 above the third.
- The augmented triad consists of a M3 and +5 above the root. This chord can also be understood as stacked thirds with a M3 above the root and a M3 above the third.
The Five Seventh Chords
The five types of seventh chords are illustrated below. The bottom note in each case is the root of the chord.
- The major seventh chord consists of a M3, P5, and M7 above the root. It can be viewed as a major triad with a major seventh or understood as stacked thirds with a M3 above the root, a m3 above the third, and a M3 above the fifth.
- The dominant seventh or major-minor seventh chord consists of a M3, P5, and m7 above the root. It can be viewed as a major triad with a minor seventh or understood as stacked thirds with a M3 above the root, a m3 above the third, and a m3 above the fifth.
- The minor seventh chord consists of a m3, P5, and m7 above the root. It can be viewed as a minor triad with a minor seventh or understood as stacked thirds with a m3 above the root, a M3 above the third, and a m3 above the fifth.
- The half-diminished seventh chord consists of a m3, o5, and m7 above the root. It can be viewed as a diminished triad with a minor seventh or understood as stacked thirds with a m3 above the root, a m3 above the third, and a M3 above the fifth.
- The diminished seventh chord (sometimes called the fully diminished seventh chord) consists of a m3, o5, and o7 above the root. It can be viewed as a diminished triad with a diminished seventh or can be understood as stacked thirds with a m3 above the root, a m3 above the third, and a m3 above the fifth.
Circle of Thirds
These chord spellings can be illustrated on the “circle of thirds,” which is a visual aid for identifying and building triads and seventh chords. The pitch classes of a triad or seventh chord are always next to one another on this circle. This graphic should be read clockwise. For example, the pitches A – C – E form a triad. The pitches B – D – F – A form a seventh chord.
Writing Triads and Seventh Chords
After the structures of these various chords are memorized, writing them becomes easy. Use your interval writing skills to your advantage. It is especially helpful to have all the white key thirds memorized.
Example: Write a minor chord on the following root.
Step #1 Fill in the needed notes above the given note. The root of this chord is E♭, so the chord will be spelled using the notes G and B.
Step #2 What type of third is G above E♭? It is a M3, so it must be lowered by one half step (semitone) to become a m3.
Step #3 You can either write a M3 above the G♭ or you can write a P5 above the E♭.
Example: Write a Mm7 chord using the given note as the fifth of the chord.
Step #1 Fill in the root, third, and seventh.
Step #2 Because the B♭ (the fifth of the chord) is given, it cannot be changed. The top interval of a Mm7 chord is a m3. Find the m3 above B♭.
Step #3 Find the m3 below B♭.
Step #4 You can either find the M3 below the G or a P5 below the B♭. Either will yield the correct answer.
Lead-Sheet Symbols, Bass Position Symbols, and Roman Numerals
Lead-Sheet Symbols, Bass Position Symbols, and Roman Numerals - Blackboard pools
- Lead-Sheet Symbols and Roman Numerals
- Lead-Sheet Symbols – Augmented Triads
- Lead-Sheet Symbols – Diminished Triads
- Lead-Sheet Symbols – Major Triads
- Lead-Sheet Symbols – Minor Triads
- Lead-Sheet Symbols – Fully Diminished Seventh Chords
- Lead-Sheet Symbols – Half Diminished Seventh Chords
- Lead-Sheet Symbols – Major Minor Seventh Chords
- Lead-Sheet Symbols – Major Seventh Chords
- Lead-Sheet Symbols – Minor Seventh Chords
Lead-Sheet Symbols
Lead-sheet symbols are a type of short-hand notation that tells the musician the root and type of chord. This system is not completely standardized in textbooks and published music, which means there are sometimes two or more accepted symbols that can represent a given chord. Lead-sheet symbols can be used to harmonize a melody. The usual custom is to place the lead-sheet symbol directly above the measures in a melody.
Lead-sheet symbols are a valuable tool in understanding and analyzing music. We will use the following lead-sheet symbols as the standard for our class.
Bass Position Symbols (Figured Bass Symbols)
Chords can appear in root position or in inversion. The lowest written note of a triad or seventh chord in root position or inversion is referred to as the bass. Root position chords feature the root as the lowest note. First inversion chords feature the third of the chord as the lowest note. Second inversion chords have the fifth of the chord as the lowest note. Seventh chords allow for a third inversion in which the seventh of the chord is the lowest or bass note.
Inversions are indicated using bass position symbols. During the Baroque period, Arabic numerals were added to bass lines to show the accompanying harmonies. Keyboard players in an ensemble would read from these “figured bass” parts and fill in the harmonies. This system of figured bass symbols is now used in music theory in a simplified form. These numbers indicate intervals above the lowest note in the texture, even if it is in treble clef. For the purposes of this chapter, we will normally assume these are simple intervals. In part-writing and analysis, however, these numbers often refer to compound intervals.
Various symbols may be combined with these bass position symbols to raise or lower a pitch. For example, a ♯ or + next to a numeral or a slash through a numeral indicates that you should raise that note by a half step. A ♭ symbol next to a number indicates that you should lower that note by a half step. The ♮ symbol can be used to raise or lower a pitch, depending on the key signature. An accidental floating by itself beneath the staff belongs to the note a third above the bass and can be used to raise or lower that note. If there are no modifying symbols next to a bass position symbol, you should use the notes found in the diatonic scale which are the accidentals found within the key signature.
The following examples show these concepts in practice.
Roman Numerals
Roman numerals have been used in the analysis of Western music for over two centuries. Roman numerals include a lot of information about chords, including root, bass position, type, and function. They are a valuable tool in understanding the harmonic element of music.
Roman Numerals in Music Theory:
- Uppercase Roman numeral = major Triad.
- Lowercase Roman numeral = minor triad.
- Uppercase Roman numeral with a “+” = augmented triad.
- Lowercase Roman numeral with a “o” = diminished triad.
- Uppercase Roman numeral with a “M7” = major seventh chord
- Uppercase Roman numeral with a “7” = major minor (dominant) seventh chord.
- Lowercase Roman numeral with a “7” = minor seventh chord.
- Lowercase Roman numeral with a “Ø7” = half-diminished seventh chord.
- Lowercase Roman numeral with a “o7” = diminished seventh chord.
Major Keys
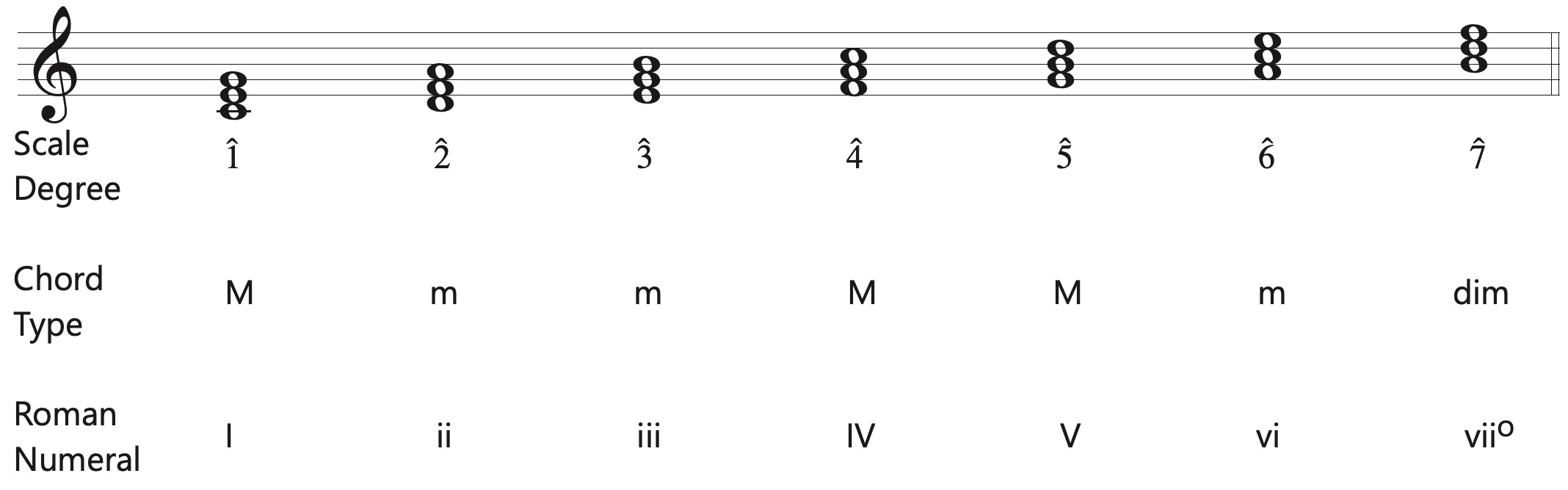
Diatonic triads built on each scale degree in major mode. This example is in the key of C major.
Diatonic seventh chords built on each scale degree in major mode. This example is in the key of C major.
Minor Keys
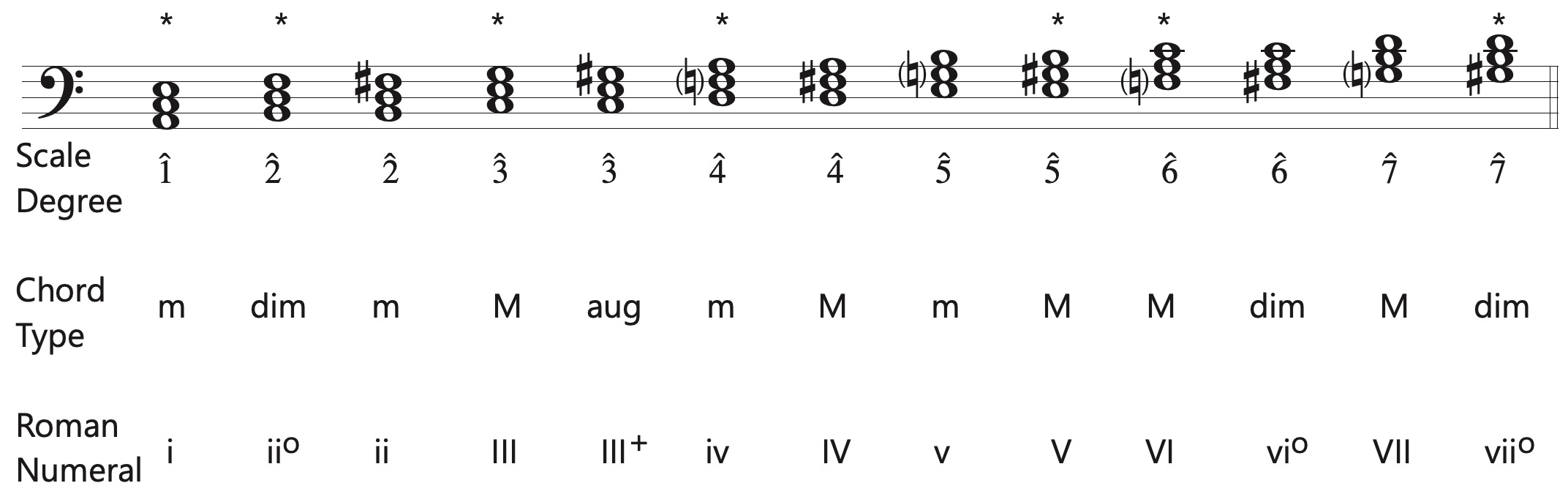
Because of the existence of harmonic and melodic minor scales, the situation in minor keys is more complicated. In minor keys, all the common triads and seventh chords are constructed using the natural minor form of the scale EXCEPT the V, V7, viio, and viio7. These utilize the leading tone or raised seventh scale degree found in the harmonic and melodic minor scales. The purpose of the harmonic minor scale is to allow the creation of the V and viio chords in minor. The third of a root position V or V7 chord will be the leading tone in the key. The leading tone will be the lowest note of a root position viio or viio7 chord.
Diatonic triads built on each scale degree in minor mode. This example is in the key of a minor. An asterisk (*) indicates the most used triads in minor keys.
Diatonic seventh chords built on each scale degree in minor mode. This example is in the key of a minor. An asterisk (*) indicates the most used seventh chords in minor keys.