Intervals
Intervals
An interval is the distance between two pitches. Intervals are harmonic when two pitches are played or sung at the same time and are melodic when two pitches are played or sung one after another in a melody. Intervals are simple when they are an octave or less in distance and are compound when they exceed an octave.
Numbers and Qualities
Intervals are identified by a number and a quality. The half step (semitone) is the smallest interval in tonal music. Any two piano keys that are next to one another are a half step apart. This pattern is most commonly a white key next to a black key, but the white key notes E to F and B to C are also half steps.
- Interval qualites include perfect (P), major (M), minor (m), augmented (+), and diminished (o).
- Generic intervals that can be perfect include the 1, 4, 5, and 8 (1 = unison and 8 = octave).
- Generic intervals that can be major or minor include the 2, 3, 6, and 7.
- Any interval can be augmented or diminished.
- Perfect intervals can be made larger or smaller by a half step.
° ↔ P ↔ + - Major and minor intervals can be made larger or smaller by a half step.
° ↔ m ↔ M ↔ +
Just as there are enharmonic spellings for notes, there are enharmonic intervals as well. The +6 sounds the same as a m7 but is spelled differently. An +6 above C is an A♯, while a m7 above C is a B♭. The A♯ and B♭ are enharmonic and are both 10 half steps (semitones) above C, but the C to A♯ is counted as a sixth and the C to B♭ as a seventh. Doubly augmented intervals can be created by expanding an augmented interval by one semitone, and doubly diminished intervals can be created by contracting a diminished interval by one semitone. Such intervals are rare in music, and we will not otherwise consider them in this text.
This is a list of commonly encountered intervals. This list is not exhaustive.
Interval Name | # of semitones |
P1 | 0 (unison) |
m2 | 1 |
M2 | 2 |
+2 | 3 |
m3 | 3 |
M3 | 4 |
P4 | 5 |
+4 | 6 (tritone) |
°5 | 6 (tritone) |
P5 | 7 |
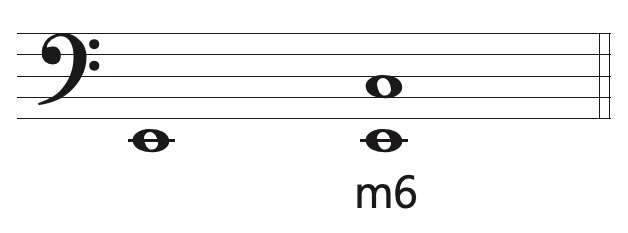
m6 | 8 |
M6 | 9 |
+6 | 10 |
m7 | 10 |
M7 | 11 |
P8 | 12 (octave) |
Identification of Intervals
Major Scale Method
There are a few ways to identify intervals. One method is to use the intervals found between scale degrees in the major scale.
Step 1 Count the interval’s numerical name. Start on the bottom note and call it “1” and continue to the top note. Do not skip a note name. In the following example, D = 1, E = 2, F = 3, G = 4, A = 5, and B = 6. The numerical name for this interval is a 6th.
Step 2 Think of the bottom note as the tonic of a major scale. Is the note “B” the normal sixth scale degree in D major? Yes, it is, which makes this a M6.
White Key Method
Another method of determining and writing intervals is called the white key method. While this does require memorizing all the intervals between the white keys of the piano, it is a powerful tool and allows very quick identification and writing of intervals.
Below are the white key seconds. Five of them are major seconds and two are minor seconds.
Next are the white key thirds. Four of them are minor thirds and three are major thirds.
These are the white key fourths. All of them are perfect except for F-B.
While fourths invert to fifths (see Interval Inversion) and can therefore be easily calculated, the fifths are included here because of their utility in building chords.
These white key intervals can be expanded or contracted by a half-step. For example, E to G is a minor third apart. If we lower the E by a semitone, the E♭ to G is now a major third apart. If we apply the same accidental to any of these white key intervals, the interval quality stays the same. For example, the notes C♮ and E♮ are a major third apart. The notes C♭ and E♭ are also a major third apart, as are the notes C♯ and E♯.
Interval Inversion
Inversion of an interval occurs when the bottom pitch is placed above the top pitch or when the top pitch is placed below the bottom pitch. To find the inversion of an interval, subtract the number of the interval from 9. The number 9 is a constant value because the sum of an interval and its inversion will always add up to 9.
7ths invert to 2nds
6ths invert to 3rds
5ths invert to 4ths
Major intervals become minor
Minor intervals become major
Perfect intervals remain perfect
Diminished intervals become augmented
Augmented intervals become diminished
By using the concept of inversion, it is easy to calculate the sixths and sevenths using the white key method. The major second between the notes C and D, for example, inverts to a minor seventh between D and C. If we make that one semitone larger, we have a major seventh between D and C♯.
Writing an Interval Above a Given Note
Major Scale Method
You can use the major scale method or the white key method for writing intervals above a given note.
Example: Write a m6 above the given note E.
Step 1 Write the note a sixth above E, using E as 1. The note a sixth above E is C.
Step 2 Think in the key of the bottom note, which is E major. The note C♯ is the sixth scale degree in the key of E major and is therefore a M6 above C. The C♮ is a m6 above E.
Sometimes you will have to write an interval above a note that is the tonic of an unusual key, such as F♭.
Example: Write a P5 above F♭
Remove the flat so that you are now thinking in the key of F. The P5 above F is C. When you add the flat back to the F, you must also add a flat to the C to maintain the P5.
Writing an Interval Below a Given Note – Inversion Method
You can use the concept of inversion to write an interval below a given note. When using the inversion method, you first invert the interval and find this interval above the given note. After this note is found, you will then place it an octave lower thus putting the note below the given pitch.
Example: Write a P4 below the given note
Consonance and Dissonance
Intervals are categorized as consonant or dissonant based on their sound and harmonic stability. Consonant intervals are more stable and “sweet” in sound. Dissonant intervals are less stable and “harsher” in sound.
Consonant harmonic intervals include the following:
- Major and minor thirds and sixths (M3, m3, M6, m6)
- Perfect intervals except the P4 (P1, P5, P8)
Dissonant harmonic intervals include the following:
- Major and minor seconds and sevenths (M2, m2, M7, m7)
- Tritones – the o5 and +4
The perfect fourth (P4) is a special case. It is dissonant when it is the first interval above the lowest note (the "bass" note). This is true when it is part of a dyad, which is when two pitches are sounding together. It is also true when it is part of a triad, which is when three pitches sound together as a chord. It is consonant, however, when it is supported by a third below it.