Twelve-Tone Serialism
Overview
Composers such as Arnold Schoenberg pushed the chromaticism of late German Romanticism to the breaking point in the closing years of the 19th century with pieces such as Transfigured Night (1899). By the first decade of the 20th century, Schoenberg moved toward atonality, in which dissonances are freed, tertian structures are abandoned, and vertical sonorities consist of any combination of intervals. This style of music fit well with Expressionism, the German visual art and literature style of the early 20th century that reflected sometimes unpleasant inner thoughts rather than pleasant scenes or pictures. Expressionism in Schoenberg’s music is exemplified in pieces such as Three Piano Pieces, Op. 11(1909), Erwartung (1909) and Pierrot Lunaire (1912).
Schoenberg developed the concepts of free or nonserial atonality until the interwar period when his first pieces using the twelve-tone method were written. In twelve-tone serialism, all the pitch classes in the chromatic scale are arranged in a tone-row (tone series) with certain restrictions applied:
- All twelve pitch classes of the chromatic scale must be used in a specific order.
- No pitch class can be repeated until the entire row has sounded, with exceptions made for immediate repetition(s) of a note.
- The series can be inverted (mirror inversion), retrograded (played backward), and transposed.
Tone-rows are typically constructed in a manner that avoids the appearance of a tonal center, tertian structures, and diatonic scales, and should be understood as a logical extension of the atonal music that historically precedes it.
Terminology
Prime – The original or prime (P) form of the row is that which appears at the beginning of a piece.
Retrograde – The retrograde (R) is the original form of the row played backwards.
Inversion – The inversion (I) is the mirror inversion of the original row.
Retrograde Inversion – The retrograde inversion (RI) is the inversion of the original row played backward.
The following examples illustrate these concepts. The prime form (P0) of the row is presented first. Note that the pitch classes can be written with sharps, flats, or a combination of these because of the enharmonic equivalence of notes such as C♯ and D♭. The numbers under the notes are the order numbers and show each note’s position in the row.
Next is the retrograde (R0), which is simply P0 backwards without transposition.
The original row can also be inverted (I0) without transposition. This technique is called mirror inversion and involves analyzing the intervals between the pitch classes in the prime row and then inverting them the same number of semitones in the opposite direction. For example, the first interval in P0 is the P4 (5 semitones) between the C and F. A P4 below C is the note G, but because of octave equivalence this G can be notated a P5 above C or the P4 below.
Retrograde inversion (RI0) is the inversion in reverse order.
Each of these four basic forms can be transposed to begin with any of the twelve pitch classes, which means each row has a total of forty-eight possible permutations. The number that follows the abbreviation (for example, P0) refers to the transposition level of the row. The label P5, for example, indicates that the prime row has been transposed up by 5 semitones and would therefore start on the note F. The label RI7 is simply stating that the retrograde inversion of the row has been transposed up by 7 semitones and would start on the note C.
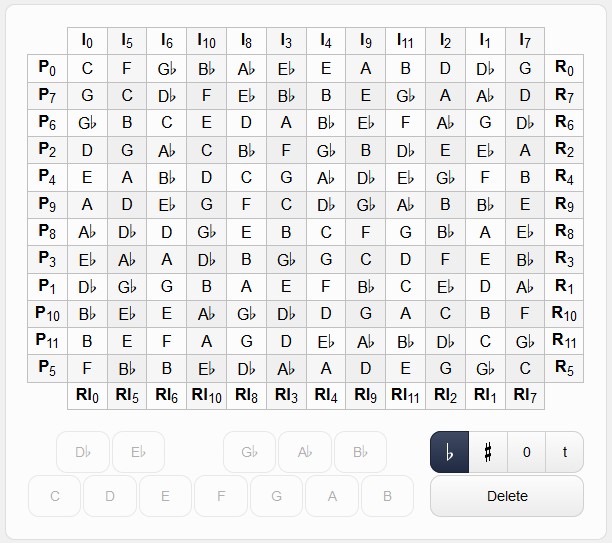
Twelve-Tone Matrix
The forty-eight possible row forms can be expressed in a 12-tone matrix, which can be generated with online tools, with a phone app, or manually filled in. There are two methods of designating the prime row. The traditional method designates the initial row form encountered in the composition as P0. For example, if a composition begins with the note E, P0 will start with E and P1 will begin a half-step above on an F. The absolute pitch method labels the row that starts on C as P0, which means a row beginning with E would have a transposition level of 4 and be designated P4, even if it were the opening row form encountered in a piece.
It is helpful to understand the process by learning to fill in the matrix manually. The following directions assume the traditional method of row identification and construction. We will use this method in our analysis of 12-tone music.
- Determine the prime row and fill in P0 in the top row of boxes.
- Write the transposition numbers above the matrix. The first pitch is 0, the note a half step above is 1, and so forth. Write these numbers underneath the matrix as well.
- Write the transposition numbers on the left side of the matrix. To find them, subtract each number on top from 12 and write that number in the corresponding space on the left. The first number is always 0.
- Write the notes in the boxes on the left side of the matrix that correspond to the numbers in P0. For example, G is 7 in P0, so it will be written in the box next to the 7 on the left of the matrix.
- Go to the horizontal row that corresponds to the number 1 and transpose P0 up a semitone into that row.
- Continue this process with the horizontal row that corresponds to the number 2, and so forth.
- The diagonal running from the top left to bottom right will always be the first note of P0 in the upper left corner of the matrix.
The following matrix is based upon the prime row discussed thus far. Prime is read left to right, Retrograde right to left, inversion top to bottom, and retrograde inversion bottom to top. This was completed using an online matrix calculator.
Rows can be further subdivided into smaller groupings of ordered notes, including trichords (three notes), tetrachords (four notes), and hexachords (six notes). Each row therefore contains four trichords, three tetrachords, and two hexachords. The interval content in each grouping can be tightly controlled, and some composers have taken advantage of these segments by limiting the intervals found in each grouping to create the same or similar pitch class sets.
In music, row forms can be used in an assortment of ways and are not always clearly shown. They can be overlapped, presented canonically, stacked vertically, and given in different instruments or voices. The first task is to identify the prime row, regardless of whether the traditional or absolute pitch method is used. In Anton Webern’s Wie Bin Ich Froh, P0 occurs in the opening measures of the piano accompaniment but notes 6-9 of the row are stacked in a vertical sonority, making it difficult to determine the correct order. In measure 3, P0 is again stated, and in measure 4 the order number of notes 6-9 becomes clear, allowing the construction of a matrix and the analysis of the row forms used in the piece. The prime row of this piece is F♯ - F♮ - D♮ - E♮ - E♭ - C♮ - A♮ - C♯ - G♯ - B♮ - B♭ - G♮, as illustrated in the next example.
Berg and Webern
Two composers who studied with Schoenberg and who developed the 12-tone method in their own ways are Alban Berg and Anton Webern. Berg and Webern’s early styles were rooted in late German Romanticism, and both followed Schoenberg into atonality and serialism. Of the two, Berg remained the most Romantic and used the twelve-tone technique more freely, as shown in the Violin Concerto, which even quotes a Bach chorale.
Webern’s influence has continued far beyond his unfortunate death during the occupation of Germany following World War II, and he became an admired figure by the post war serial composers. Webern was strict in his use of the twelve-tone method, and his music is highly concentrated, with some movements less than a minute long. His music is noted for its use of soft dynamics, pointillistic and transparent textures, brilliant orchestration, the use of special effects (mutes, harmonics, flutter tonguing), a reliance on canonic writing such as the double canons in the Symphony Op. 21 (1928), and tightly organized and highly atonal tone rows.
Integral Serialism
Integral or total serialism is an extension of twelve-tone technique, particularly that of Webern, who was a primary model for the post WWII serial composers such as Karlheinz Stockhausen and Pierre Boulez. Integral serialism can include the serialization of rhythm, dynamics, register, articulation, row form, and timbre, and shows the search for the total control over all aspects of music. Another significant figure in this technique was Milton Babbitt, who originated the concept of using a matrix (or “square”) to list the 48 permutations for a given 12-tone row.