1.5 Fibonacci numbers

Overview
| TCCNS Course | MATH 1332: Contemporary Mathematics |
| UT Austin Course | M 302: Introduction to Mathematics |
Introduction
Suggested Resources and Preparation
Materials and Technology
- Piles of sticks, coins, or even bits of modeling clay can be used to play Fibonacci nim.
Prerequisite Assumptions
The derivation of the Golden Ratio from the Fibonacci sequence requires some fraction manipulation and the Quadratic Formula.
Students should be able to write simple logical arguments using cases.
Overview and Student Objectives
Lesson Length
100 minutes (two 50 minute class periods recommended)
Lesson Objectives
Students will understand that:
- The Fibonacci numbers are a sequence of integers generated using a recursive formula.
- The sequence of ratios of consecutive Fibonacci numbers has a limit, called the Golden Ratio.
Students will be able to:
- Use recursive formulas to generate sequences of numbers.
- Look at a table of values for a sequence and form a conjecture about the limit of that sequence.
- Play the game of Fibonacci nim.
- Describe the algorithm by which a player may win Fibonacci nim.
- Analyze games of Fibonacci nim and determine whether moves made were strategically optimal or not.
Fibonacci numbers and the Golden Ratio
Video: Plants grow in spirals! (sometimes)
What's the pattern?
| Object | CCW Spirals | CW Spirals |
|---|---|---|
| Pinecone A | 5 | 8 |
| Pinecone B | 8 | 13 |
| Yellow daisy | 13 | 21 |
| White daisy | 21 | 34 |
| Sunflower | 34 | 55 |
| ??? | 55 | ??? |
Question: Can you extend the pattern? What numbers come after 55?
Fibonacci Sequence
The Fibonacci Sequence is an infinitely long list of numbers that you generate by adding the previous two to get the next one. We traditionally start with two 1's:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, ...
A long list of fractions leading to a pattern
Let's say we took this infinitely long list of numbers and created a list of fractions out of them. The pattern we will use is putting each number in the list above the previous number:
\(\frac{1}{1},\frac{2}{1},\frac{3}{2},\frac{5}{3},\frac{8}{5},\frac{13}{8},\frac{21}{13},\frac{34}{21},\frac{55}{34},\dots\)
Next, we can take these fractions and calculate their decimal approximations. When we do this, we see a pattern emerge:
| Fraction | Decimal |
|---|---|
| \(\frac{1}{1}\) | 1 |
| \(\frac{2}{1}\) | 2 |
| \(\frac{3}{2}\) | 1.5 |
| \(\frac{5}{3}\) | 1.666... |
| \(\frac{8}{5}\) | 1.6 |
| \(\frac{13}{8}\) | 1.625 |
| \(\frac{21}{13}\) | 1.615... |
| \(\frac{34}{21}\) | 1.619... |
| \(\frac{55}{34}\) | 1.618... |
| \(\frac{89}{55}\) | 1.618... |
The decimals appear to be getting closer together and are "leveling off" at some number. This is what's known as a limit and that limit has a name: the Golden Ratio.
But what exactly is the Golden Ratio? What if we want to know it precisely and not just to three decimal places?
Making fractions out of Fibonacci numbers
Turning the fractions into compound fractions, then into a special number
Golden Ratio
The Golden Ratio is a number that gets the name \(\varphi\) (a cursive phi, pronounced "fee"). It is exactly equal to \(\frac{1+\sqrt{5}}{2}\) and it is approximately equal to 1.618...
Fibonacci nim
Fibonacci nim is a two-player game that is a variant of the classic nim game. Remember that when we talk about games in this course, we are usually trying to figure out if one player has an advantage over the other, and if so, we want to write down exact instructions on how to "hack" the game or always win.
Fibonacci nim rules
- You can play this game starting with any number of sticks you want.
- For the first move only, Player 1 can choose any number of sticks between 1 and n-1. In other words, they can't take 0 and they can't take all of them.
- For every move after the first move, the player can choose any number of sticks between 1 and twice as many as the last number taken. If Player 1 takes 2 sticks, then Player 2 can take between 1 and 4. If Player 2 takes 4 sticks, then Player 1 can choose 1, 2, 3, 4, 5, 6, 7, or 8 sticks.
- The player who takes the last move and grabs the last stick(s) wins. The last move does not have to be a one-stick move.
"Beating" a game
What does it mean to beat a game? We would need to answer these types of questions:
- Does either player have a definite advantage?
- Is it always guaranteed that one of the players can win if they play with a certain strategy?
- If so, what is that optimal play strategy?
- If there is no guaranteed strategy, what strategies maximize the chances of winning?
For example, in Tic Tac Toe, some of us have learned that if you are Player 1, or X, then you can always win or draw if you play a certain way. If you are Player 2, or O, and if Player 1 is playing smart, then the best you can hope for is a draw. But what about this nim game?
Example game
Let's look at an sample game starting with 20 sticks, just to get used to the rules.
| Moves allowed | Move taken | Sticks left |
|---|---|---|
| Player 1 can choose 1-19 | 4 | 16 |
| Player 2 can choose 1-8 | 5 | 11 |
| Player 1 can choose 1-10 | 2 | 9 |
| Player 2 can choose 1-4 | 3 | 6 |
| Player 1 can choose 1-6 | 6 | 0 |
Player 1 wins!
Question: Did Player 2 make a mistake? If so, where?
Looking for patterns
If you look at the last turn that Player 2 took, where they could choose 1-4, notice that they chose 3, which allowed Player 1 to take all the remaining sticks. The same thing would have happened if they'd taken 4. But this wouldn't have happened if they had chosen 1 or 2 sticks. So I feel confident labeling that move as a mistake.
Go back to the very first move and take the perspective of Player 1. There are 20 sticks?
- If Player 1 takes 19 sticks, what can Player 2 do?
- If Player 1 takes 18 sticks, what can Player 2 do?
- If Player 1 takes 17 sticks, what can Player 2 do?
- If Player 1 takes anywhere from 7-16 sticks, what can Player 2 do?
The answer to all of these questions "They will just take the rest and win." This is because you always get to take up to twice as many as the last move. There's a pattern here.
Claim: No player should ever take 1/3 of the sticks or more in any turn.
Proof: If one player takes 1/3 or more of the sticks, then the other player is allowed to take up to 2/3. That's all of the sticks. The other player will win.
Small problem though: I want specific instructions for winning. So far, in a 20 stick game, all I know is that I shouldn't take 7 or more. But which of the moves 1-6 is best?
Too many cases
The math skill that I believe is most useful here is reducing the problem. As in, we will write a similar but much easier problem that we can solve and then build up to the original problem. Here, 20 seems very large and complicated. So I will pick something small to start. What happens if we play a game with just 2 sticks?
Claim: In a two stick game, Player 2 will always win.
Proof: Player 1's only choice is to take one stick. Player 2 can then take the other stick.
Let's build up from there.
Claim: In a three stick game, Player 2 will always win.
Proof: Player 1's only choice is to take one stick. Player 2 can then take the other two sticks.
Claim: In a four stick game, Player 1 will always win.
Proof: Player 1's only strategic choice right now is to take one stick. There are three remaining, and Player 2 can choose either one stick or two sticks. Either way, Player 1 will win on the very next turn.
Claim: In a five stick game, Player 2 will always win.
Proof: Player 1's only strategic choice right now is to take one stick. This means that Player 2 can choose one or two sticks; they should definitely choose one stick. Then there are three sticks remaining, and Player 1 knows that no matter what they do they will lose on the next turn.
Question: Can you keep going with games of 6-13 sticks?
A pattern emerges
Here are some initial results of these experiments. In cases where Player 1 has the advantage, I've also listed the first move that guarantees a win.
| Size of game | Player with advantage | First move |
|---|---|---|
| 2 | 2 | |
| 3 | 2 | |
| 4 | 1 | 1 |
| 5 | 2 | |
| 6 | 1 | 1 |
| 7 | 1 | 2 |
| 8 | 2 | |
| 9 | 1 | 1 |
| 10 | 1 | 2 |
| 11 | 1 | 3 |
| 12 | 1 | 1 |
| 13 | 2 |
The crazy result is that every time a game start with a Fibonacci number, Player 2 has the advantage. If the game starts with a non-Fibonacci number, Player 1 has the advantage. Also notice that the optimal moves tend to be very small. Trying to speed up a game by taking more sticks is risky.
Finally notice that in many cases, Player 1's winning first move is to make Player 2 take a Fibonacci number of sticks. This is a key insight.
But first! Some math!
Every positive number is a sum of non-adjacent Fibonacci numbers
- Pick the biggest Fibonacci number you can that is still smaller than your number.
- Subtract the Fibonacci number from your number.
- Repeat the process with your new smaller number until you get to zero.
Example 1
Write 120 as a sum of non-adjacent Fibonacci numbers.
Write down some Fibonacci numbers:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233,...
- The largest one that is less than 120 is 89, and 120-89=31.
- The largest Fib. number that is less than 31 is 21, and 31-10=10.
- The largest Fib. number that is less than 10 is 8, and 10-8=2.
2 is a Fib. number, so 120=89+21+8+2.
Notes
- Let's consider 1 and 2 adjacent, even though there are two ones.
- If you find a sum using adjacent Fibonacci numbers, you can combine them to make a better sum. For example: 120=55+34+21+8+2, and those are all Fibonacci numbers, but we can combine the 55+34=89.
Now we can use this skill to "hack" Fibonacci nim.
The punchline: a winning strategy
- If the game is starting with a Fibonacci number of sticks, then Player 2 has the advantage. If the game is starting with a non-Fibonacci number of sticks, then Player 1 has the advantage.
- Never take 1/3 of the sticks or more. In general, it is desirable to make your opponent receive a Fib. number of sticks.
- To do this, in every turn, you want to express the number of sticks left as a sum of non-adjacent Fibonacci numbers (as in, not next to each other in the Fib. sequence), then choose the smallest.
Example game
In a 20 stick game, Player 1 should have the advantage. Let's play using the strategy
| Moves allowed | Best option | Sticks taken | Sticks remaining |
|---|---|---|---|
| Player 1 can choose 1-19 | 2 because 20=13+5+2 | 2 | 18 |
| Player 2 can choose 1-4 | No best option because 18=13+5 | 4 | 14 |
| Player 1 can choose 1-8 | 1 because 14=13+1 | 1 | 13 |
| Player 2 can choose 1-2 | No best option because 13 is Fib number | 2 | 11 |
| Player 1 can choose 1-4 | 3 because 11=8+3 | 3 | 8 |
| Player 2 can choose 1-6 | No best option because 8 is Fib number | 3 | 5 |
| Player 1 can choose 1-6 | 5 because they'll win! | 5 | 0 |
Extra Resource
This Fibonacci nim player from Dr. Andrew Long at Northern Kentucky University will help you play lots of rounds of the game.
Quiz Questions
| Question | Answer |
| 1 | 3 |
| 2 | 2 |
| 3 | 1 |
| 4 | 3 |
| 5 | 1,2 |
Question 1
What are the next 3 Fibonacci number after 1,1, 2, 3, 5?
- 7, 9, 11
- 8, 12, 17
- 8, 13, 21
- 6, 7, 8
Question 2
Make a list of numbers obtained by taking each Fibonacci number, squaring it and adding it to the next Fibonacci number squared. Here are the first few entries in your list:
\(1^2+1^2=2\)
\(1^2+2^2=5\)
\(2^2+3^2=13\)
Can you see a pattern to the resulting numbers?
- The answer is the square of a Fibonacci number.
- The list consists of every other Fibonacci number.
- The list cannot go on.
- There is no pattern.
Question 3
What is the Golden Ratio exactly?
- \(\frac{1+\sqrt{5}}{2}\)
- \(1+\frac{\sqrt{5}}{2}\)
- 1.6
- \(\frac{34}{21}\)
Question 4
Let's say we are playing a game of Fibonacci nim with 32 sticks, and I am Player 1. What should my opening move be?
- 1 because you always start with 1
- 11 because then Player 2 will get 21 sticks and they'll definitely lose.
- 3 because 32=21+8+3
- 1 because 32=21+8+2+1
Question 5
So in a game of Fibonacci nim with 15 sticks, Player 1 takes 1 stick, then Player 2 takes 2 sticks, then Player 1 takes 1 stick. This means that Player 2 has 11 sticks left.
Which of these moves were mistakes? Select all that apply.
- Player 1's first move
- Player 2's first move
- Player 1's second move
Homework Questions
Question 1.5.1
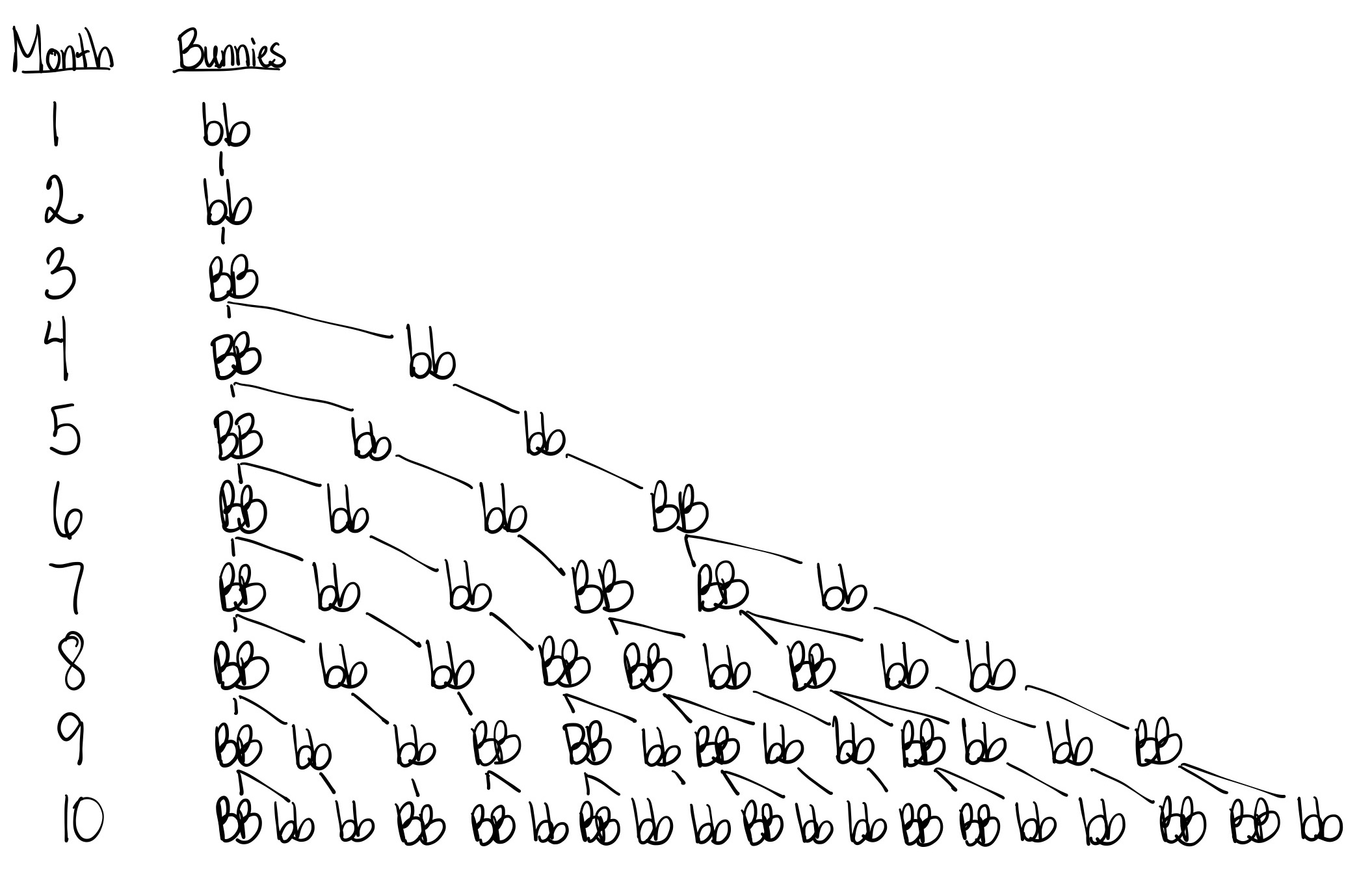
In the nth month there will be a number of pairs equal to the nth Fibonacci number. Students may choose to express that in words "In each month you can find the number of pairs by adding the previous two numbers together," or may choose an algebraic presentation.
Question 1.5.2
| Month | # Pairs |
| 0 | 1 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 6 |
| 6 | 9 |
| 7 | 13 |
| 8 | 19 |
| 9 | 28 |
| 10 | 41 |
Students can use plain English to describe the pattern: "To get the number of pairs in month n, just add the number of pairs from one month ago to the number from three months ago."
Question 1.5.3
- Starting with 2,1, you get: 2,1,3,4,7,11,18, 29, 47, 73, 120, 193, 313, 526, 839.
- The quotients approach the Golden Ratio again.
- Answers vary. The quotients always approach the Golden Ratio.
- The starting terms don't appear to play any role at all.
Question 1.5.4
- The Tribonacci numbers are 1,1,2,4,7,13,24,44,81,149,274,504,927,1705,3136,...
- Quotients approach an irrational number that is approximately 1.839...
- The quotients do approach a fixed number that is not the Golden Ratio. They don't have to prove what it is.
Question 1.5.5
We get a mirror image of the Fibonacci sequence only every other number is negative:
..., 13, -8, 5, -3, 2, -1, 1, 0, 1, 1, 2, 3, 5, 8, 13,...
Question 1.5.5
Express each of the following numbers as a sum of non-adjacent Fibonacci numbers: 32, 245, 406, 3000.
\(32=21+8+3\)
\(245=233+8+3+1\)
\(406=377+21+8\)
\(3000=2584+377+34+5\)
Question 1.5.6
Count the number of sticks that are left. Express that number as a sum of non-adjacent Fibonacci numbers. Choose the smallest.
If you are beginning the game with a Fibonacci number of sticks and you are Player 2, this will work. If you are beginning the game with a non-Fibonacci number of sticks and you are Player 1, this will work.
I am not aware of any other strategy that works in 100% of cases. Students will sometimes want to take several of the smallest Fibonacci numbers. This works in some cases, but we never worked out exactly which cases.
Question 1.5.7
There are 37 sticks remaining, and 37 = 34+3. Player 1 can choose from 1-4 sticks, and they should pick 3.
Question 1.5.8
60 = 55+5. Player 1 should have taken 5 sticks. Since they took 4 sticks, now Player 2 has 56 sticks, and 56=55+1. They can take 1 stick and leave you with a Fibonacci number.
Question 1.5.9
36 = 34 + 2. First move was smart.
36 - 2 - 4 = 30, 30 = 21 + 8 + 1, second move was a mistake. You should have taken 1.
30 - 2 - 3 = 25, 25 = 21 + 3 + 1, third move was a mistake. You should have taken 1.
Question 1.5.10
The only possible "smart moves" are 1 and 2, since you should never take 1/3 of the sticks. So we have to do two cases.
- If Player 1 takes one stick, then Player 2 will take 2 sticks, since 7 = 5 + 2. Then Player 1 has 5 sticks. The only move that is less than 1/3 of the sticks is one sticks. If Player 1 takes one stick, then Player 2 will have 4 sticks. They will choose 1. Then Player 1 can choose 1 or 2 sticks out of 3.
- If Player 1 takes one stick, Player 2 will take the rest of the sticks and win.
- If Player 1 takes two sticks, Player 2 will take the last stick and win.
- If Player 1 takes two sticks, then Player 2 will take one stick, since 6 = 5 + 1. Player 1 will have 5 sticks. We already argued this case above; no matter what, Player 1 will lose.
Question 1.5.11
The only possible "smart moves" are 1 and 2, since you should never take 1/3 of the sticks. So we have to do two cases.
- If Player 1 takes one stick, then Player 2 will take 2 sticks, since 7 = 5 + 2. Then Player 1 has 5 sticks. The only move that is less than 1/3 of the sticks is one sticks. If Player 1 takes one stick, then Player 2 will have 4 sticks. They will choose 1. Then Player 1 can choose 1 or 2 sticks out of 3.
- If Player 1 takes one stick, Player 2 will take the rest of the sticks and win.
- If Player 1 takes two sticks, Player 2 will take the last stick and win.
- If Player 1 takes two sticks, then Player 2 will take one stick, since 6 = 5 + 1. Player 1 will have 5 sticks. We already argued this case above; no matter what, Player 1 will lose.
Question 1.5.1
Suppose we have a pair of baby rabbits: one male and one female. Let us assume that rabbits cannot reproduce until they are one month old and that they have a one-month gestation period. Once a pair starts reproducing, they produce one pair of bunnies each month (one of each sex). Assuming that no pair ever dies, how many pairs of rabbits will exist in each month?
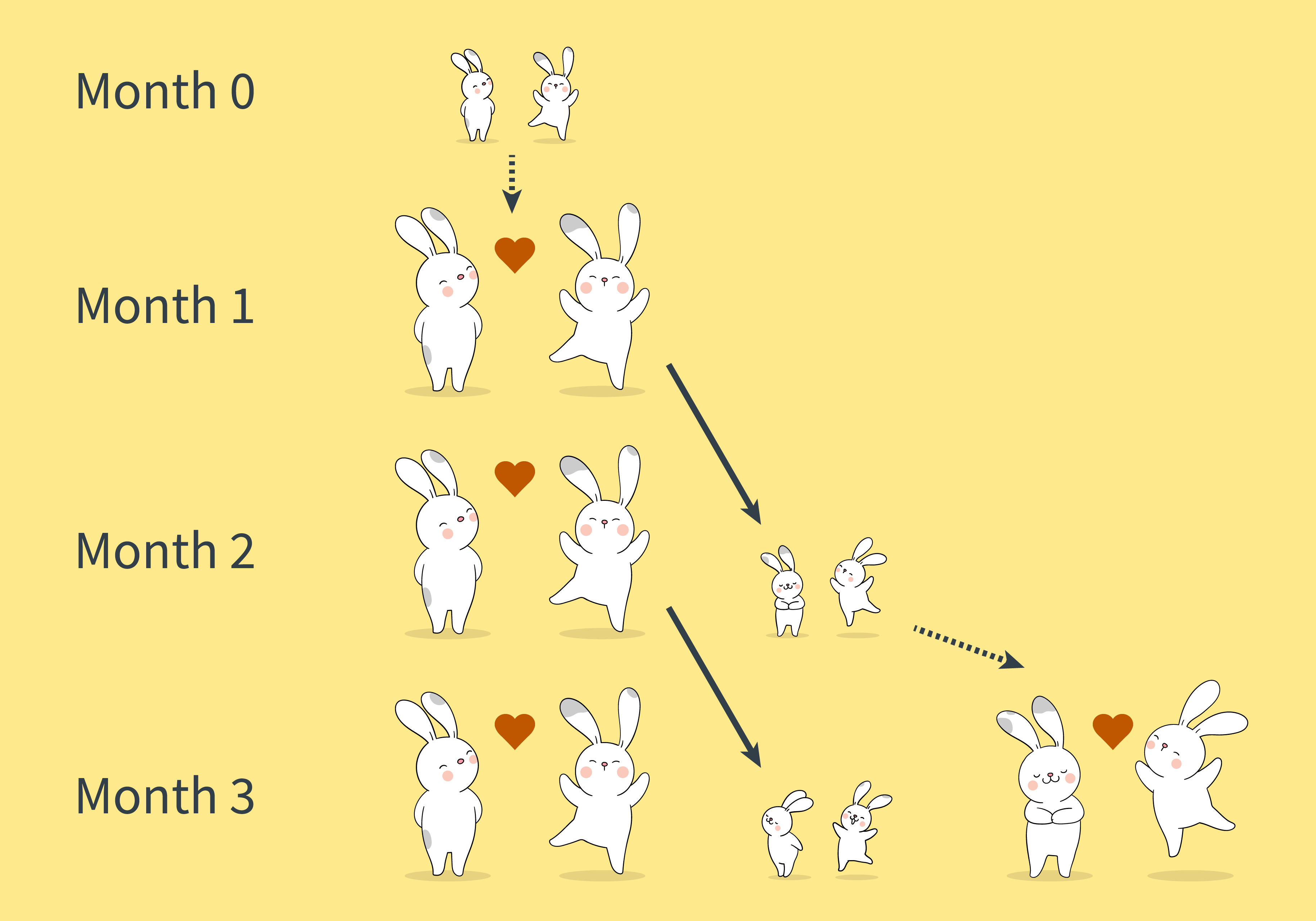
Question 1.5.2
Suppose we start with one pair of baby rabbits, and again they create a new pair every month, but this time let's suppose that it takes two months before a pair of bunnies is mature enough to reproduce.
- Make a table for the Months 0 through 10, indicating how many pairs there would be at the end of each month.
- Do you see a pattern? If so, describe it.
- Describe a general formula for generating the sequence of rabbit-pair counts.
Question 1.5.3
Suppose we build a sequence of numbers using the method of adding the previous two numbers to build the next one. This time, however, suppose our first two numbers are 2 and 1. (This sequence is called the Lucas sequence.)
- Generate the first 15 terms.
- Compute the quotients of consecutive terms of the Lucas sequence as we did with the Fibonacci numbers. What number do these quotients approach?
- Pick two positive numbers and use those as your first two terms to generate a sequence. What do the quotients approach?
- In conclusion, what role do the initial values play in determining what number the quotients approach?
Question 1.5.4
Let's start with the numbers 0, 0, 1, and generate future numbers in our sequence by adding up the previous three numbers.
- Write out the first 15 terms in this sequence, starting with the first 1.
- Use a calculator to evaluate the value of the quotients of consecutive terms (dividing the the larger number by the smaller number).
- Do the quotients seem to be approaching a fixed number? (You don't need to prove this item, just make an observation).
Question 1.5.5
Is it possible to extend the pattern of the Fibonacci numbers backwards? Try to write ten numbers that come before the two 1's, and describe the pattern that you see:
..., _, _, _, _, _, _, _, _, _, _, 1, 1, 2, 3, 5, 8, 13, ...
Question 1.5.6
Express each of the following numbers as a sum of non-adjacent Fibonacci numbers: 32, 245, 406, 3000.
Question 1.5.7
Describe the "magic strategy" that we discussed in class that ensures you will win Fibonacci nim in most cases. In which cases does the magic strategy work?
Question 1.5.8
Suppose you are playing Fibonacci Nim with your friend and you are starting with 40 sticks. You are Player 1. You take 1 stick, then your friend takes 2. What valid moves do you have to choose from? How many sticks should you take next to win?
Question 1.5.9
Suppose you are playing Fibonacci Nim with your friend and you are starting with 60 sticks. You are Player 1. You take four sticks as your first move. Why was this a mistake? What should Player 2 do to win the game?
Question 1.5.10
Suppose you are playing Fibonacci Nim with your friend and you are starting with 36 sticks. You take 2 sticks, your friend takes 4 sticks, you take 2 sticks, your friend takes 3 sticks, then you take 2 sticks. Were any of your three moves mistakes, or were they all "smart" moves?
Question 1.5.11
Suppose you are playing Fibonacci Nim with your friend and you are starting with 8 sticks. You are Player 1. Write a proof that it is impossible to win the game as long as Player 2 is following the "magic strategy." Hint: use cases.
Application to your life
Background
Exploring the natural numbers was an exercise in looking back on something we take for granted and seeing what impulses might have generated that familiar idea. By looking at where a concept came from, we can look for inspiration on how to take that concept further than ever before.
Here we want you to apply that technique to some issue in your own life. Have you ever been asked by an instructor "Do you have any questions?" Or perhaps have you been assigned a research project and didn't even know where to start? Being able to brainstorm questions is a key skill in life that will benefit you for years.
Reading
If you need some help getting started, you might consider reading this piece from Open Colleges:
Learning to Ask Better Questions: 12 Tricks
Assignment: Ask questions
First, choose an issue to think about. The "issue" that you consider can be a current event, a decision you are having to make in your personal life, a historical event, or a current issue as in a political issue. Write down the issue. If it's specialized at all, like your instructor might not know what it is, you may want to briefly describe it.
Next, formulate at least three different questions about where that issue or topic or decision came from. Just the questions, not the answers. Imagine that you are beginning a big term paper on this issue and you are choosing things you could research. Focus on origins of this issue.