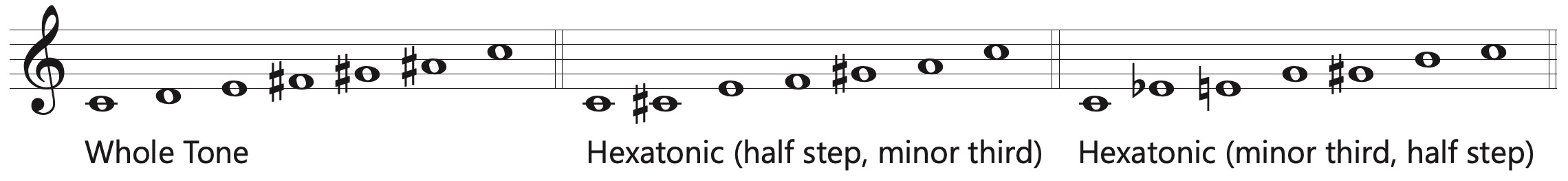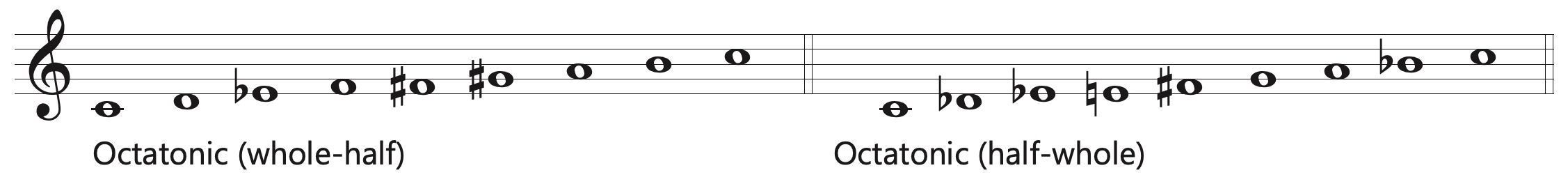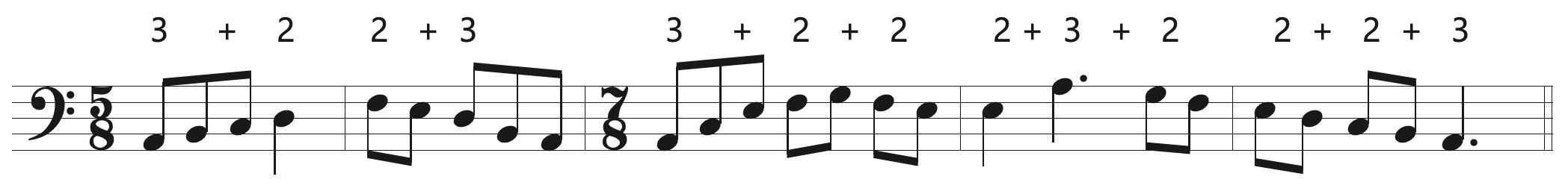- Author:
- Stephen Emmons
- Subject:
- Performing Arts
- Material Type:
- Textbook
- Level:
- Academic Lower Division
- Tags:
- License:
- Creative Commons Attribution Non-Commercial Share Alike
- Language:
- English
Education Standards
Augmented Sixth Chords and Enharmonic Modulation - exercises
Harmony - exercises
Other Chromatic Harmonies - analyses
Other Chromatic Harmonies exercises
Rhythm in the 20th Century - exercises
Scales in the 20th Century - analysis
Scales in the 20th Century - exercises
Transposing Instruments exercises
Twelve-Tone Serialism - analyses
Twelve-Tone Serialism - exercises
A Survey of Music Theory for the College Classroom: Chromatic Harmony 2 and 20th Century Music

Overview
A Survey of Music Theory for the College Classroom is a concise, practical, and readable text and workbook for use in the freshman and sophomore music theory curriculum.
Introduction
A Survey of Music Theory for the College Classroom is a concise, practical, and readable text and workbook for use in the freshman and sophomore music theory curriculum. The text is divided into four parts which are linked by a table of contents, allowing for a seamless transition between them.
A Survey of Music Theory for the College Classroom: Fundamentals
A Survey of Music Theory for the College Classroom: Diatonic Harmony
A Survey of Music Theory for the College Classroom: Chromatic Harmony I
A Survey of Music Theory for the College Classroom: Chromatic Harmony II and 20th Century Music
Most chapters include PDFs of exercises and excerpts for analysis. I encourage the instructor to supplement the course materials through the analysis of lengthy excerpts or complete pieces of music, especially during the sophomore year. I also highly recommend the use of Rising Software’s Musition (theory) and Auralia (aural skills) software. The Musition and Auralia software package is robust, customizable, and can be used to reinforce most concepts covered in freshman and sophomore theory. I have also written a comprehensive set of exams as well as about 1100 objectives questions for use in Blackboard. Please email me at semmons@angelo.edu from a valid faculty email address if you would like to access these tests or Blackboard pools.
In addition to the extensive excerpts for analysis, the reader will note the prevalence given to part-writing, especially in the books Diatonic Harmony and Chromaticism I. In my experience, part-writing is the laboratory in which the student can learn many of the fundamentals of music theory. Additionally, I have found that students enjoy and even prize the time spent at the boards actively learning through part-writing and the completion of similar in class exercises.
The examples from the literature in the text and workbook were taken from the IMSLP that are public domain in the United States. I wrote all the part-writing and short examples in the text, all the exercises for the workbook, and a few pieces for analysis that demonstrate various techniques.
I dedicate this book to the late Dr. Edward Pearsall and the late Dr. Mary Jeanne van Appledorn. I studied Schenkerian analysis and 20th century theory with Ed during my doctorate at Texas Tech. Through these classes and as a member of my dissertation committee, he had a profound influence on my understanding of music and on my writing. Dr. Van was one of a kind. I studied composition and theory with her during my doctorate, and she was a master teacher of composition, the use of scales, and the music of Debussy. I have happy memories of sitting with her at the piano banging through my music or analyzing various 20th century works. She taught with great care and with humor. I shall always be in her debt.
Stephen D. Emmons, Ph.D.
Table of Contents
A Survey of Music Theory for the College Classroom: Fundamentals
- Pitch, Scales, and Keys
- Intervals
- Rhythm, Meter, and Beaming
- Triads and Seventh Chords
- Lead-Sheet Symbols and Roman Numerals
A Survey of Music Theory for the College Classroom: Diatonic Harmony
- Harmonic Progression
- Texture, Voice Leading and Counterpoint
- Root Position Part-Writing
- First Inversion Triads
- Second Inversion Triads
- Cadences and Small-Scale Form
- Nonchord Tones
- Second and Fourth Species Counterpoint
- Dominant Seventh Chords
- Leading Tone Seventh Chords
- Nondominant Seventh Chords
A Survey of Music Theory for the College Classroom: Chromatic Harmony I
- Secondary Dominants
- Secondary Leading Tone Chords
- Modulation
- Binary and Ternary Form
- Borrowed and Neapolitan Chords
A Survey of Music Theory for the College Classroom: Chromatic Harmony II and 20th Century Music
Transposing Instruments
Transposing Instruments - Blackboard pools
- Transposition pool for Theory
I have also developed several Blackboard pools for my orchestration class that cover transposition. Please email me at semmons@angelo.edu if you would like to have these.
Overview
Transposing instruments produce pitches that sound different from what is notated in the score. There are several reasons for the existence of transposing instruments, including the following:
- Ease of notation because of extremely high or low range.
- Player’s convenience, fingering systems, and families of instruments
- History and tradition.
- Sound quality and intonation.
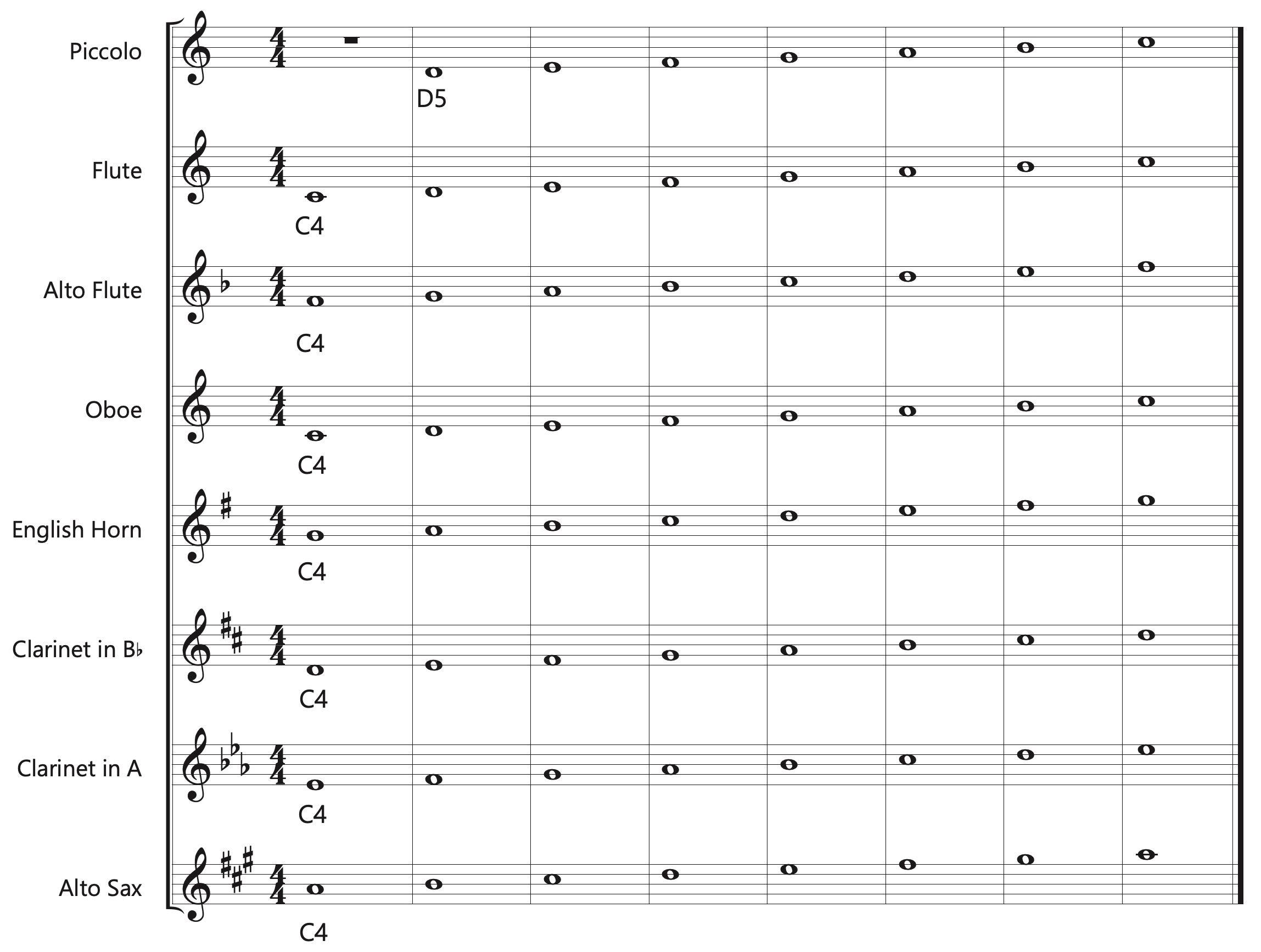
Transposition Examples
The following examples consist of C major scales and show how transpositions appear for the most common wind, brass, and string instruments in the band and orchestra. The sounding (concert) pitch is indicated below each tonic note. Observe how the key signatures are different for the transposing instruments. For example, the clarinet in B♭ sounds a M2 lower than written, so must be written up a M2 to match a given concert pitch or key. This means that to play in concert C major, the clarinet in B♭ must be written in the key of D major.
High Woodwinds
Low Woodwinds
High Brass
Low Brass
Strings
Transpositions for Common Band and Orchestral Instruments
Instrument | Written Pitch in relation to the concert/sounding pitch | Clef |
Piccolo | Down a Perfect Octave | Treble |
Flute (C flute) | Non-transposing | Treble |
Alto Flute (in G) | Up a Perfect 4th | Treble |
Oboe | Non-transposing | Treble |
English Horn | Up a Perfect 5th | Treble |
Bassoon | Non-transposing | Bass and Tenor |
Contrabassoon | Up a Perfect Octave | Bass |
E♭ Clarinet | Down a minor 3rd | Treble |
A Clarinet | Up a minor 3rd | Treble |
B♭ Clarinet | Up a Major 2nd | Treble |
E♭ Alto Clarinet | Up a Major 6th | Treble |
B♭ Bass Clarinet | Up a Major 9th | Treble |
E♭ Contra Alto Clarinet | Up a Perfect Octave and a Major 6th | Treble |
B♭ Contrabass Clarinet | Up 2 Perfect Octaves and a Major 2nd | Treble |
B♭ Soprano Saxophone | Up a Major 2nd | Treble |
E♭ Alto Saxophone | Up a Major 6th | Treble |
B♭ Tenor Saxophone | Up a Major 9th | Treble |
E♭ Baritone Saxophone | Up a Perfect Octave and a Major 6th | Treble |
C Trumpet | Non-transposing | Treble |
B♭ Trumpet | Up a Major 2nd | Treble |
Flügelhorn | Up a Major 2nd | Treble |
Horn in F (French Horn) | Up a Perfect 5th | Treble and Bass |
F Alto Horn, Mellophonium | Up a Perfect 5th | Treble |
Baritone (Treble Clef) | Up a Major 9th | Treble |
Baritone (Bass Clef) | Non-transposing | Bass |
Tenor Trombone | Non-transposing | Bass and Tenor |
Bass Trombone | Non-transposing | Bass |
Euphonium | Non-transposing | Bass |
Tuba | Non-transposing | Bass |
Sousaphone | Non-transposing | Bass |
Orchestral Bells (Glockenspiel) | Down 2 Perfect Octaves | Treble |
Chimes (Tubular Bells) | Non-transposing | Treble |
Xylophone | Down a Perfect Octave | Treble |
Marimba | Non-transposing | Treble and Bass |
Timpani | Non-transposing | Bass |
Piano | Non-transposing | Treble and Bass |
Harp | Non-transposing | Bass and Treble |
Violin | Non-transposing | Treble |
Viola | Non-transposing | Alto and Treble |
Violoncello | Non-transposing | Bass, Tenor and Treble |
Contrabass | Non-transposing | Bass |
Augmented Sixth Chords and Enharmonic Modulation
Augmented Sixth Chords and Enharmonic Modulation - Blackboard Pools
- Augmented Sixth Chords and Enharmonic Modulation
- Fr+6
- Ger+6
- It+6
Overview
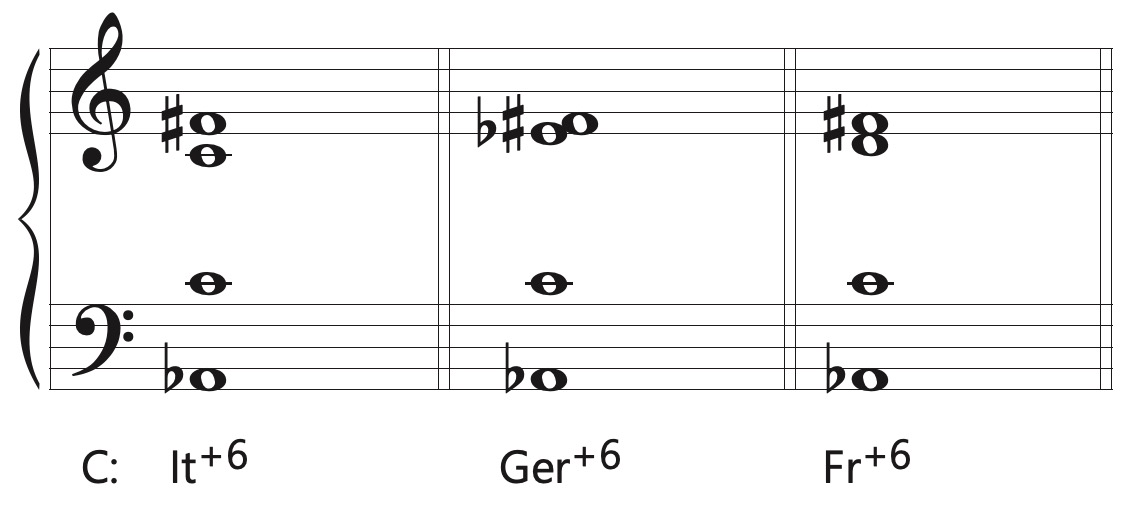
Augmented sixth chords are another class of chromatic chords that are used by composers to enrich harmonic textures and propel motion toward the dominant and tonic chords. Two of these chords, the German augmented sixth (Ger+6) and the Italian augmented sixth (It+6) are enharmonically spelled Mm7 chords, while the French augmented sixth chord (Fr+6) is an entirely new structure and sound type in our studies. The reasons for the names of these chords lay in the distant past, and no geographic meaning should be attached to them.
Augmented sixth chords have a strong predominant function, replacing either the subdominant or supertonic harmonies in motion toward the dominant chord, and are typically preceded in progressions by supertonic, subdominant, and submediant chords. Augmented sixth chords can also be used as dominant substitutes that progress directly to the tonic chord, and more rarely will be used to tonicize something other than the dominant or tonic chords in a key. We will explore each of these prospects in turn.
By far the most typical use of an augmented sixth chord is as a predominant function. The augmented sixth arises because the tonicized note is approached simultaneously by notes a half step above and half step below. When inverted, this o3 becomes an +6, and the resolution is outward to the octave. When progressing to the V chord, this characteristic interval consists of the ♭\(\hat{6}\) and ♯\(\hat{4}\).
To these two altered scale degrees the It+6 adds the tonic scale degree, the Ger+6 adds the tonic and ♭\(\hat{3 }\), and the Fr+6 adds the tonic and supertonic scale degrees. Keep in mind that the ♭\(\hat{3 }\) and ♭\(\hat{6}\) are already present in minor keys.
Part-Writing Augmented Sixth Chords
The part-writing guidelines for augmented sixth chords are not difficult. All predominant augmented sixth chords resolve directly to the V or to a I64 – V, and the♭\(\hat{6}\) scale degree is usually found in the bass. The interval of the +6 should resolve outward to the octave, with the other chord tones exhibiting smooth voice leading. When writing It+6 chords in SATB textures, the tonic note is to be doubled. Please note the interesting exception to the use of parallel fifths that arises when the Ger+6 progresses to V.
When an augmented sixth chord resolves directly to a V7, the top note of the +6 resolves to the 7th of the V7, as shown in the last example.
Occasionally the ♯\(\hat{4}\) is in the bass rather than the ♭\(\hat{6}\). This inverts the +6 to a o3, and the usual resolution is for this interval to collapse inward to the unison or octave. Note again the parallel fifths that occur when the Ger+6 progresses directly to V.
Atypical It+6, Ger+6, and Fr+6 Chords
Augmented sixth chords occasionally substitute for dominant harmonies and progress directly to the tonic chord. Augmented sixth chords more rarely progress to a scale degree other than the tonic or dominant. We will adopt the analysis practices of the secondary dominant and leading tone chords when analyzing these uses of the +6 chord, for example It+6/I(i), Ger+6/I(i), Fr+6/I(i), It+6/IV, Ger+6/ii, Fr+6/VI, and so forth. Note that some theorists prefer using scale degrees for these occurrences of +6 chords rather than roman numerals, for example It+6/\(\hat{1}\), Ger+6/\(\hat{1}\), Fr+6/\(\hat{1}\). As with secondary functions, only scale degrees that can serve a tonic function can be tonicized with an augmented sixth chord.
Spelling +6 chords that progress to something other than the dominant can be a little trickier than usual. The following procedure can be applied to any instance in which the +6 tonicizes a scale degree other than the dominant.
- Find X, the note (scale degree) to be tonicized.
- Go down a P5 and act as if X is the dominant in the key a P5 below X.
- Build the +6 chord to X in that key using the same technique we learned when building pre-dominant +6 chords.
- Semitone above/semitone below tonicized note + tonic scale degree in key = It+6
- Semitone above/semitone below tonicized note + tonic scale degree in key + scale degree ♭\(\hat{3}\) = Ger+6
- Semitone above/semitone below tonicized note + tonic scale degree in key + scale degree \(\hat{2}\) = Fr+6
In the following example, the tonic scale degree in C/c is being tonicized. Go down a P5 from C to F and build the +6 chord as if it were progressing to the dominant in the key of F/f.
Some theorists conceive of augmented sixth chords as altered chords, which is useful when analyzing or constructing the most common occurrences of these chords. When progressing to the dominant chord or scale degree, the following is seen:
- The It+6 can be considered as a IV built on the ♯\(\hat{4}\) and with a ♭\(\hat{6}\) (the ♭\(\hat{6}\) is already present in minor mode).
- The Ger+6 can be considered as a IV7 built on the ♯\(\hat{4}\) and with a ♭\(\hat{6}\) and ♭\(\hat{3}\) (the ♭\(\hat{6}\) and ♭\(\hat{3}\) are already present in minor mode).
- The Fr+6 that can be considered as a II7 with a with a ♯\(\hat{4}\) and ♭\(\hat{6}\). (the ♭\(\hat{6}\) is already present in minor mode).
Likewise, when progressing to a tonic triad or scale degree, the following is seen:
- The It+6/I (i) can be considered as a VII with a ♭\(\hat{2}\).
- The Ger+6/I (i) can be considered as a VII7 with a ♭\(\hat{2}\) and ♭\(\hat{6}\).
- The Fr+6/I (i) can be considered as a V7 with a ♭\(\hat{2}\).
Enharmonic Modulation
Enharmonic equivalence references the point that there are more than two spellings for any given note. Obvious examples are the notes C♯ and D♭, but less common ones such as E♮ and F♭ are to be found. Similarly, we can take advantage of enharmonic spellings to reinterpret chords in different keys. Enharmonic modulation takes advantage of the fact that o7 and Mm7 (Dom7) chords can be resolved in diverse ways. Each o7 chord can resolve in four different ways, and each Mm7 chord can resolve in two different ways.
Fully Diminished Seventh Chords
We will begin by studying o7 chords. Because o7 chords are comprised only of m3 intervals, they are “aurally inversionless.” The B in the following chord is the leading tone to C. It is therefore a viio7 in C/c.
Even when the chord is inverted on paper, the aural result is that of stacked m3 intervals. In the following example, note that the A♭ to B is an +2, which is enharmonic with a m3.
Because of this quality, each chord member can serve as the leading tone to the pitch a semitone above it. This means that it is as valid to hear the Bo7 chord resolve to the keys of A/a, G♭, or E♭/e♭ or their enharmonic equivalents as it is to the key of C/c. Composers take advantage of this aural ambiguity to effect modulation to foreign keys.
The D in this chord is the leading tone to E♭ and is now a viio42 in E♭/e♭. If you play the chord at the piano, it still looks like you are playing the notes B, D, F and A♭. This is the essence and power of enharmonic modulation.
The F in this chord is now the leading to G♭, so it is now a viio43 in G♭. We would need to enharmonically spell the chord to take it to F♯ major or f♯ minor (E♯ G♯ B D), which is enharmonic to G♭.
The A♭ cannot be the leading tone to B♭♭ because B♭♭is not a “real” key. We must enharmonically spell the A♭ as a G♯, which now serves as the leading tone to A. It is now a viio65 in A/a.
Keep in mind that any of the examples above can also serve as secondary leading tone functions. The tonicized notes can in themselves be the dominant, subdominant, and so forth of a new key.
Dominant Seventh Chords
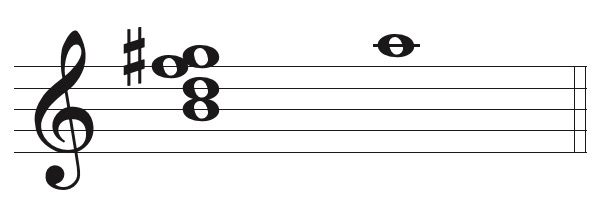
The enharmonic usage of the Mm7 is simpler than those for the o7. The Ger+6 chord is merely a Mm7 spelled enharmonically. In the following example, a garden variety C7 serves as the dominant function to F. This F could be the tonic of a key, or it could be the target of a secondary function in another key.
In the next example, the m7 between the root and the seventh has been respelled as an +6. It is now a Ger+6 that leads to the note B, which is the dominant of E/e. While it is possible for the Ger+6 to progress to something other than the dominant V chord in the new key, this is an uncommon usage in enharmonic modulation.
As with the o7 chord, these enharmonically spelled Mm7 chords can help smooth over modulations to foreign keys. Whether o7 or Mm7/Ger+6 chords are used, they may be spelled in the old key or in the new key. Because these are a type of common chord modulation, the method of identifying them with brackets, key names, and Roman numerals is the same.
When analyzing enharmonic modulation, it is important to ascertain the key to which the piece is moving. Try to find dominant functions – cadential six-four chords are especially helpful – and then back up a chord to locate the exact point of modulation.
The following example illustrates how enharmonic reinterpretation can be used to effect enharmonic modulation to distant keys. In each case the sonority is first used in its typical function – as a o7 and Dom7 in the respective keys – and then as a o7 and Ger+6 in the new keys.
Neapolitan Chords in Enharmonic Modulations
Neapolitan chords can also be spelled enharmonically to effect modulation to remote keys. In the next example, the Neapolitan chord is spelled enharmonically to produce a modulation up a semitone. The N6 chord may be spelled in the old key, enharmonically in the new key, or with elements of both as in the next example.
Modal Borrowing in Enharmonic Modulations
Modal borrowing can be used to create colorful modulations, and sometimes enharmonic reinterpretation can be used in conjunction with this. The next example is from the second movement of Beethoven’s Piano Sonata Op. 13 No. 8. After a PAC in the tonic key of A♭ major in measure 36 (note that measure numbers appear at the end of the measure in this example), Beethoven changes mode to a♭ minor in measure 37. By measure 44 we find a PAC in E major. Beethoven leverages a♭minor, the parallel minor of the tonic key of A♭ major, to effect modulation to E major, which is the enharmonically spelled submediant key (F♭ major) of a♭ minor. A♭major and F♭ major stand in a chromatic mediant relationship.
A♭ – a♭ (mm. 37-41) -- F♭/E (mm. 41-45)
Other Chromatic Harmonies
Other Chromatic Harmonies - Blackboard pools
- Other Chromatic Harmonies
Overview
We now examine several other chords that can be found within the tonal music system that do not fit any of the previous categories of chromatic harmony. While these chords are not as common as the other chromatic chords we have studied, they are used with some frequency in music of the Romantic period. Except for the cto7 chord, they can all be used as substitutes for diatonic harmonies.
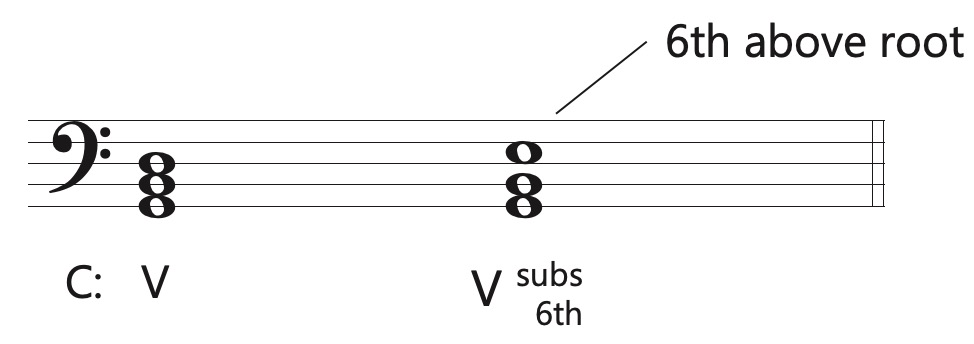
Dominant with Substituted 6th
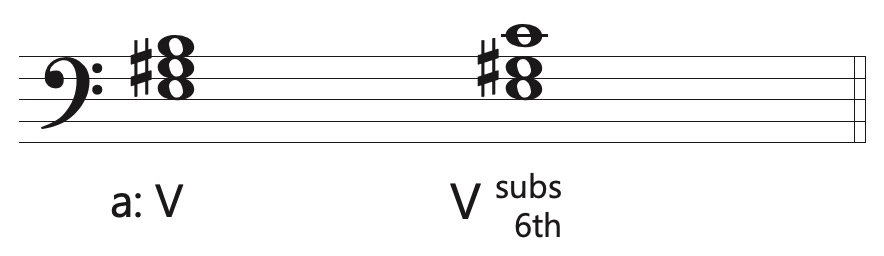
The first of these harmonies is not technically a chromatic chord because it merely involves the substitution of scale degrees in the diatonic scale. In the dominant chord with substituted 6th, the 6th above the root is substituted for the 5th above the root. You can simply “unplug” the 5th of the dominant chord and insert the 6th above the root in its place. Decades ago, some theorists used to recognize this as a iii6 chord, but in modern theory we do not do so because of the strength of the dominant motion in the bass. The Vsubs 6th substitutes for V and V7 chords, and can be approached with subdominant harmonies, including secondary dominants.
The V subs 6th can also be used in minor keys, and the result in an augmented chord sound type.
The dominant seventh with substituted 6th (V7 subs 6th) is also found. The resolution of the substituted 6th is typically by leap down to the tonic, and the seventh of the chord will resolve down by step.
Augmented Dominant Chords
Although the augmented mediant triad exists within the harmonic minor scale, the III+ chord is not used in tonal harmony. The augmented sonority, however, is sometimes used as a dominant function. Augmented dominant chords (V+) are built by raising the fifth of a regular dominant chord, which forms the leading tone to the third of the tonic chord in major keys. A m7 can be added to the V+ to create the V+7, and this chord is also used with some frequency. In part-writing, the seventh of the chord resolves down, the raised fifth resolves up to the third of the next chord, and the resolution of the leading tone can be either up to the tonic – if the leading tone is an outer voice – or down to the fifth of the next chord if the leading tone is in an inner voice.
Note that in a V+ in minor mode the altered note is enharmonically the same note as the resolution, which is the reason this chord is not used in minor keys. Observe also that the resulting sonority is identical with the dominant with substituted 6th, which can function in minor keys because the resolution is different.
Augmented dominants and augmented dominant seventh chords can also occur as secondary functions, for example V+/IV and V+7/IV.
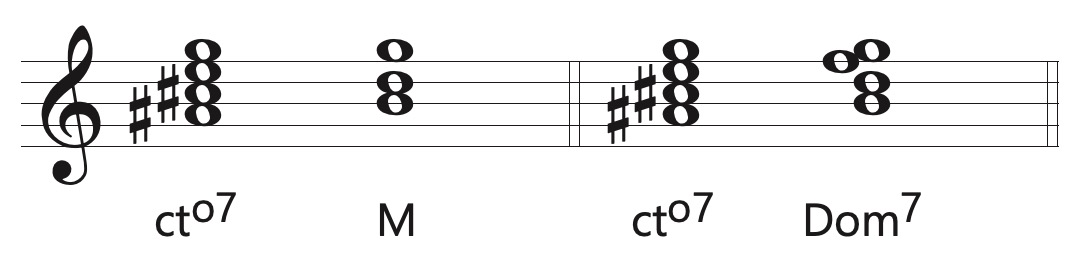
Common Tone Diminished Seventh Chords
Common tone diminished seventh chords (cto7) have a weak harmonic function and should be viewed as embellishing chords or decorations for the stronger functional harmonies around them. Common tone diminished seventh chords progress to either major triads or Dom7 (Mm7) chords, which are themselves most often either tonic or dominant harmonies within the key and which may be inverted. The root of the major or Dom7 chord to which the cto7 is progressing is a common tone with one of the notes in the cto7. Technically, the cto7 can be spelled in any fashion, but they are usually spelled with the common tone as the 7th of the cto7 chord and with stepwise motion in the other voices. Another way of looking at cto7 chords is as a collection of chromatic and diatonic neighbor or passing tones that by happenstance form a o7 chord.
Follow these steps to write cto7 chords:
- Find the root of the chord that you are embellishing and make that the common tone.
- Spell a diminished seventh chord using this common tone as the seventh.
- The other notes of the cto7 chord will form upper and lower neighbors to the embellished chord.
When part writing common-tone diminished chords in an SATB texture, the goal should be smooth voice leading, although leaps in inner voices are acceptable. An alternate to leaping is to double the fifth of the chord the cto7 is embellishing, as shown in the next examples.
Ninth Chords
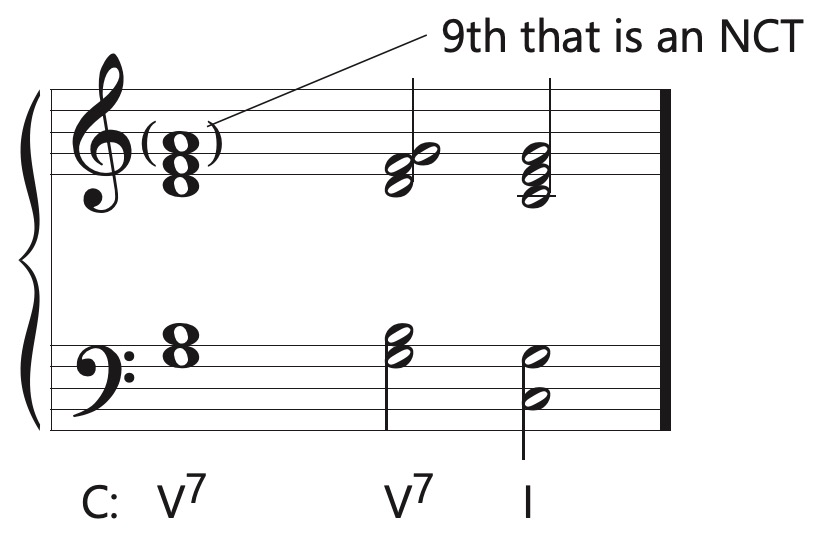
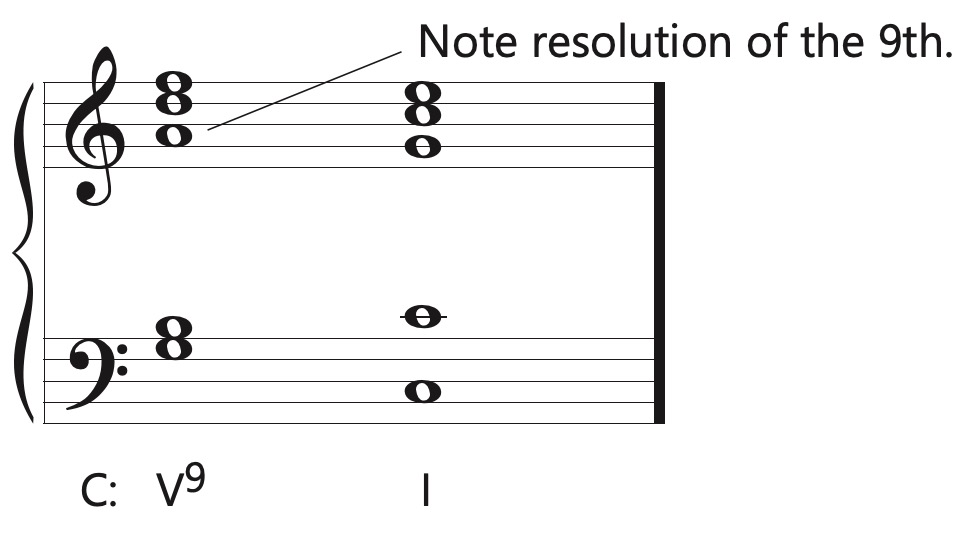
While not common in tonal music, ninth chords do occur beginning in the late Classical era. In most cases, what may be perceived as a ninth chord is merely an NCT that resolves or “dissolves” into a seventh chord. In the following example, the 9th is treated as an NCT and resolves down to the G prior to the resolution to the I chord.
In Schumann's song Ich Grolle Nicht, a borrowed iiØ7 in m. 3 moves to what at first appears to be a V♭9, but the ninth resolves into the texture at the end of the measure, showing that it is just a 9-8 suspension.
When the resolution of the 9th is delayed until the next chord, the result is clearly an actual 9th chord rather than an NCT.
The V9 (MmM) is the diatonic dominant ninth in major keys. In minor keys the V♭9 (Mmm) is found, and this sonority can be created in major by borrowing the ♭6. Whether in major or minor modes, the V♭9 (Mmm) is the most common type of dominant ninth.
Nondominant ninths are rarely used in tonal music. The most usual nondominant ninths are based on the supertonic (ii9) and subdominant (IV9 or iv9) scale degrees. Other uses of 9th chords and similar “tall chords” are discussed later in 20th Century Harmony.
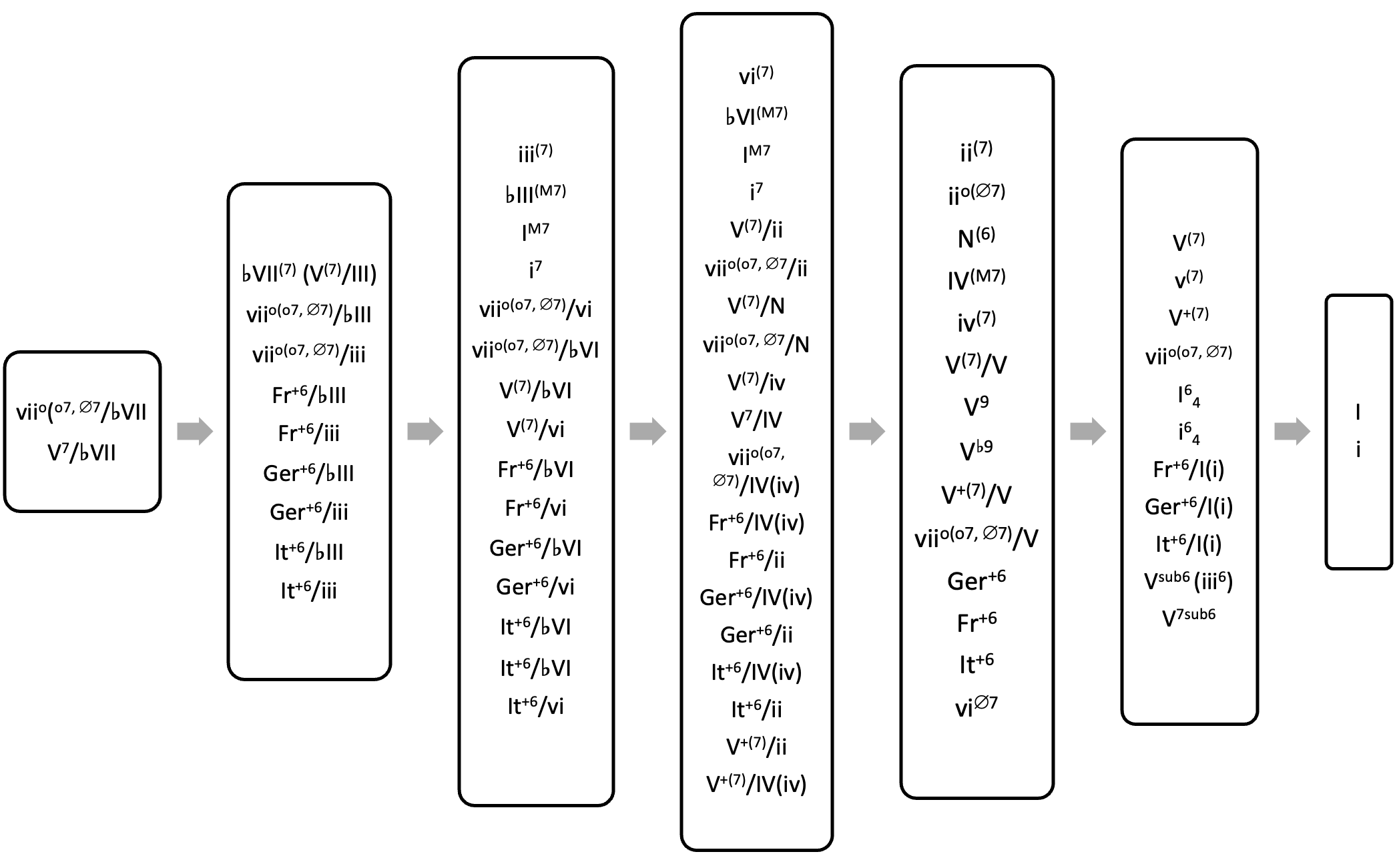
Enlarged Chart of Harmonic Progression
The addition of secondary dominant and leading tone chords, borrowed chords, augmented sixth chords, and the various chords found in this chapter greatly expands the possibilities within the chart of harmonic progression. The following chart, while not exhaustive, does illustrate the rich selection of chords available within tonal music since the dawn of the Romantic period.
Scales in the 20th Century
Scales in the 20th Century - Blackboard pools
- Scales in the 20th Century
Overview
One of the fundamental changes that occurred in music beginning in the 19th century was the use of scales outside of the major and minor scales upon which music had been based since the beginning of the Baroque period. Some of these scales were harvested from folk music, others from the Medieval and Renaissance periods, and some were simply created anew. The American composer and pedagogue Mary Jeanne van Appledorn strongly emphasized the usefulness of scales in her composition pedagogy. She noted that the various vertical sonorities and melodic options found within a given scale could be used with great freedom because of their relation to the same pitch constellation, which made them sound inherently logical and musical.
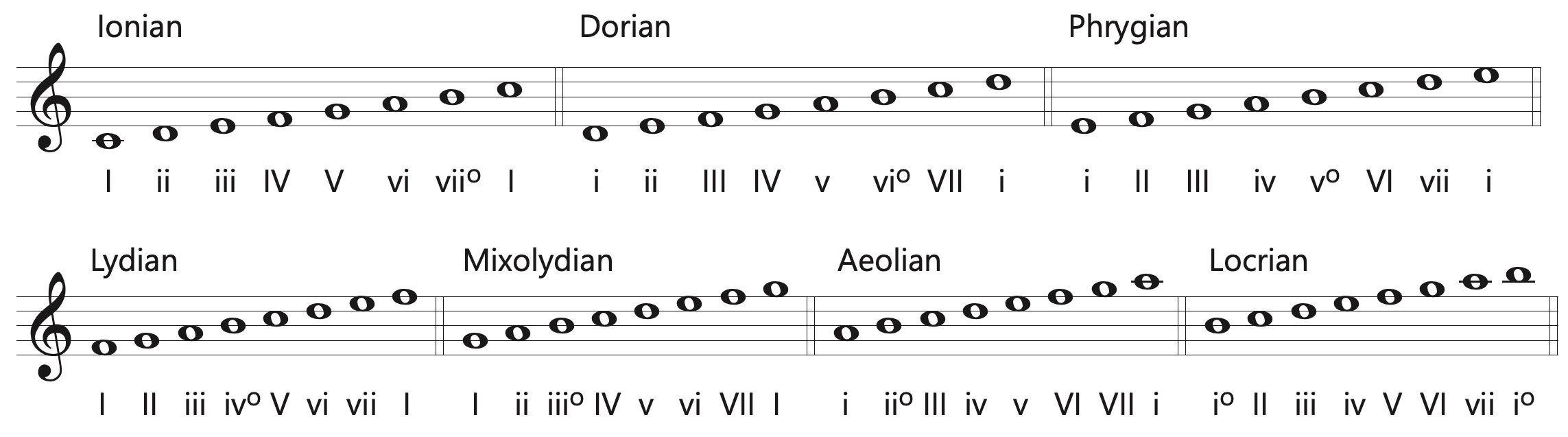
Church Modes
The diatonic or “church” modes share their names with the church modes used during the Medieval and Renaissance periods, but with a different underlying theoretical system. There are seven of these modes, all of which contain seven notes, and these scales – except for the Locrian – have been widely used in European folk music and in 20th century art music. It is possible to write the diatonic modes with any note as the finalis, but for pedagogical reasons they are often shown built on the tones of the diatonic C major scale, as illustrated in the next example. The Roman numerals show the various triad types built on each scale degree of the seven church modes. Observe that the Locrian scale has an unstable diminished triad as the tonic chord, which is why that mode is not often used outside of jazz.
The following example is in C Ionian and features only root position chords. The avoidance of functional harmonic progression is what distinguishes this from a chord progression in C major and is also what gives it a fresh and unexpected sound.
The next examples demonstrate how progressions based on the roots in the circle of fifths progression would appear in several of the church modes. Not featured are the Ionian mode, which has the same chord qualities as the major scale, and the Locrian mode, which has an unstable io chord and is thus little used. Play these at the piano and note the radically different sound the modal harmonies give to each progression.
Dorian
i – III – vio – ii – v – i
IV – VII
Phrygian
i – III – VI – II – vo – I
iv – vii
Lydian
I – iii – vi – II – V – I
ivo – vii
Mixolydian
I – iiio – vi – ii – v – I
IV – VII
Aeolian
i – III – VI – iio – v - i
iv – VII
Béla Bartók's Mikrokosmos, a collection of nearly two hundred educational piano pieces and exercises, illustrates the use of some of these scales (Phrygian, Dorian, Lydian, and Mixolydian) as well as a variety of 20th century compositional techniques.
Hybrid Scales
It is also possible to create hybrid scales by combining the tetrachords of two different modes. The bottom tetrachord of the Phrygian-Dorian comes from the Phrygian scale, while its top tetrachord comes from the Dorian scale. The bottom tetrachord of the Lydian-Mixolydian comes from the Lydian scale, and its top tetrachord comes from the Mixolydian scale. These hybrid scales further enrich the available sound color possibilities for both melodies and harmonies.
Pentatonic Scales
The pentatonic scales have also been used by composers in the 20th century but are more importantly the scales on which so much folk music across the world has been based. The American composer Lou Harrison referred to the pentatonic scale as the “human song” because of its frequent use in folk music from around the globe. The lack of a leading tone and of any m2 intervals in the major pentatonic scale leads to open sounding harmonies and the ability to effectively make any note within the scale the tonal center. These diatonic pentatonic scales occur naturally on the black keys of the piano, and a fun and rewarding experience is to practice “black key improvisation” using only these notes. Even when sounded together, the notes of the major pentatonic scale are not very dissonant because of the lack of half steps and the leading tone.
Any of the five notes in the major pentatonic can serve as the finalis or tonal center of the scale, and these five modes are expressed in the next example.
Three other pentatonic scales occur with some frequency. The minor pentatonic is drawn from the natural minor scale (observe that it is the same as mode 5 of the major pentatonic), the Kumoi pentatonic from the Dorian scale, and the Hirajoshi pentatonic from the natural minor scale.
Synthetic Scales
The more commonly encountered synthetic scales include the whole tone and hexatonic scales, each of which has six tones. The hexatonic scale can be looked at as interlocking augmented triads or as a collection of half steps and minor thirds, while the whole tone scale is made entirely of whole steps. Perhaps the most famous use of the whole tone scale is in the outer sections of Debussy’s piano piece Voiles. The middle section of this piece, which is in ternary form, uses only the black key pentatonic scale.
Octatonic scales are further examples of synthetic scales and consist of alternating half and whole steps. The standard octatonic scale exists in two versions or modes, one that begins with a whole step and one that begins with a half step.
These synthetic scales and their associated harmonic vertical sonorities have been used by composers since the 19th century, including Nikolai Rimsky-Korsakov, Claude Debussy, Modest Mussorgsky, and Igor Stravinsky. Mussorgsky uses an octatonic scale as the raw material for the harmonies and ostinatos in the Coronation Scene from the opera Boris Gudonov, as exemplified below.
Tetrachords, Pentachords, and Hexachords (Scales)
Tetrachords, pentachords, and hexachords are stepwise groupings of notes. An interesting example of the use of pentachords in a bitonal setting is found in Bartok’s Mikrokosmos, No. 86, Two Major Pentachords. The famous hymn Holy Manna features a C pentatonic melody in the tenor in what is an overall Ionian hexachord scale context, with only the treble and alto lines articulating the F and with all voices entirely avoiding the leading tone.
Nonwestern Scales
This text includes just a sample of what is possible when church modes, the scales of Western and non-Western folk music, synthetic scales, and other global resources are used. The possibilities become even greater when using tuning systems other than equal temperament that divide the octave into pitches and intervals not found in modern western scales. For example, the scale formations in traditional African music (Britannica, YouTube) include some that feature more or less evenly spaced divisions of the octave into five, six, and seven note scales. Further examples of such scales include the pelog (YouTube) and slendro (YouTube) scales used in Indonesian gamelan (Britannica, YouTube) music and the ragas (YouTube) of Carnatic (Britannica, YouTube) and Hindustani (Britannica, YouTube) music. Some scales, such as the pelog and slendro, have westernized spellings to fit them into the pitches of the standard chromatic scale, as shown in the list of scales below.
Following are forty-four scales based on the note C4. Some scales are provided with the alternate names that you will at times find in theory texts, on the internet, and in music theory software such as Rising Software's Musition.
Harmony in the 20th Century
Harmony in the 20th Century - Blackboard pools
- Harmony in the 20th Century
Pitch/Tonal Centers
It is common for 20th and 21st century music to be based on a central tone but to otherwise avoid the harmonic functions found in traditional tonality. Music that has a tonal center but that lacks traditional harmonic functions is called pitch-centric. Pitch-centric music may utilize a variety of scales as well as tertian and nontertian sonorities. Methods for establishing a pitch center include the following:
- First and Last – the pitch center is used as the first and last note in a passage or piece.
- Repetition – the pitch center is repeated.
- Accent – the pitch center appears on metrically accented beats.
- Length – the pitch center is written with longer note lengths in strategic places, textures, or timbres.
- Pedal or drone – the pitch center appears as a pedal point or as a drone
- Ostinato – the pitch center occurs as an important pitch within an ostinato.
- Dynamic – the pitch center has a louder dynamic or is accented.
- Register – the pitch center is placed as the most prominent note in the texture, such as the highest or lowest pitch.
- Modal function – the pitch center is reinforced by modal voice leading relationships such as movement from a subtonic to the tonic.
- Harmonic function – the pitch center is paired with its dominant note a P5 above or P4 below.
- Melodic function – the pitch center is paired with a leading-tone to tonic (\(\hat{7}\)-\(\hat{1}\)), subtonic to tonic (\(\hat{7}\)-\(\hat{1}\)), or supertonic to tonic (\(\hat{2}\)-\(\hat{1}\)) melodic motion.
An example of pitch centric music that has primarily modal underpinnings is Debussy’s Sunken Cathedral. While different pitch centers and scales are explored in the piece, it clearly ends with C as the pitch center. Another example is the opening movement of Stravinsky’s Symphony of Psalms, which centers on the note E while using a variety of modal and synthetic scales.
Pandiatonicism
Pandiatonicism emerged as a response to the highly chromatic and atonal music of the late 19th and early 20th centuries and is most often associated with Neoclassicism. The term is difficult to define because practices vary widely, but characteristics or definitions of pandiatonic music can include the following:
- The notes of the diatonic scale are used very freely and in a way that does not promote tonal harmonic progression based on the circle of fifths, tonal melodic voice-leading practices, and the conventional resolution of dissonances.
- Chords may be tertian or nontertian in construction.
- A tonal center may or may not be implied.
- The scales are usually in major mode, giving the music a bright, open sound that is the opposite of atonal or other highly chromatic music.
- Key signatures or accidentals may be used, or the music may exclusively feature the “white keys” on the piano.
- Ostinatos are sometimes found, and these may be layered upon one another to create dissonant and rich textures.
Examples of pandiatonicism include Alfredo Casella’s Valse Diatonique, Aaron Copeland’s Appalachian Spring, Sergei Prokofiev’s Piano Concerto No. 3, Stravinsky’s ballet Petrushka in the Russian Dance and the Shrovetide Fair tableaux.
Extended Tertian Chords
Although relatively rare, ninth chords (Mmm and MmM) have been used since the beginning of the 19th century. It was not until the early 20th century that the use of 11th and 13th chords became common. The subsequent example illustrates several extended chords built on C as well as recommended lead-sheet symbols. This list is by no means exhaustive in scope.
These “tall chords” or “extended chords” as 9th, 11th, and 13th chords are sometimes called, can be used in functional progressions (circle of fifths) and in nonfunctional successions. In functional progressions, they can substitute for triads and seventh chords, and in nonfunctional successions of chords can be used as color chords and in planing. The next example shows a circle of fifths progression in C with 9th, 11th, and 13th chords substituting for simpler diatonic triads and seventh chords.
Maurice Ravel’s Rigaudon from Le Tombeau de Couperin opens with a IVM7 – ii11 – V13 – I progression in C major in the first two measures. Gabriel Faure’s Après un Rêve features several fine examples of the use of ninth chords, and an example in the last measure of the Russian Dance from Petrushka exemplifies the use of extended chords in a tonal cadence. The progression is a ii11 (missing the third but with reinforcement of the supertonic D in the original score) – V11 – Iadd6 in C major.
Added Note Chords
Added note tertian chords are formed when a 2nd, 4th, or 6th are added above the root. Added note chords can be used to add color to an otherwise standard tonal progression to create a distinctly modern sound. Because of the strong dominant to tonic bass motion, the added 6th in the final chord in the next illustration is clearly a Iadd6 and not an inverted seventh chord.
Depending on how these chords are voiced, the effect can be that of a 9th or 11th chord with supporting thirds omitted. Because of the voicing, the Iadd2 and Iadd4 in the ensuing example could be seen as incomplete I9and I11 chords respectively, but the absence of the supporting 7th in the first example and the supporting 7th and 9th in the second example certainly weakens the sound and interpretation of these as tall chords.
Debussy’s Canope from Preludes, Book II, includes examples of added note chords as well as other techniques discussed in this chapter.
Chords with Split Thirds
A split third chord or mixed third chord includes both the major and minor third and is built on the same root, thus creating a dissonant m2. It is possible to split other members of a triad or seventh chord, but this is not as common. Examples of split third chords occur in the opening Debussy’s La Puerta del Vino. Note that the B♮ serves as the 7th of a D♭7 chord, and the E and F are the split thirds.
The next example illustrates a few possibilities for voicing a split third chord.
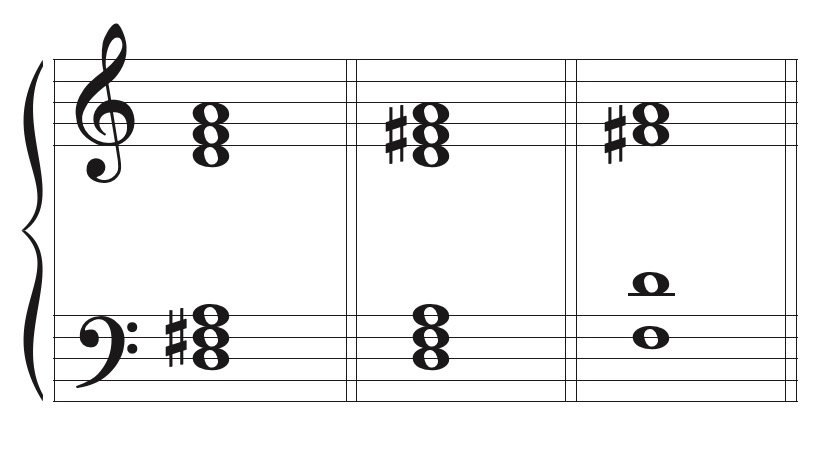
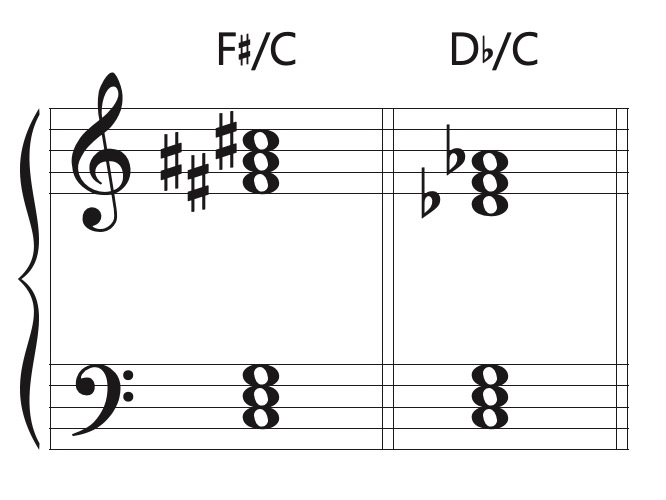
Polychords and Polytonality
Polychords come about when two or more distinct tertian chords (chordal units) – specifically triads and seventh chords – are sounded at the same time. Polychords can be written as vertical sonorities or in a linear manner. The “Petrushka chord” used by Stravinsky in the ballet Petrushka, consists of two triads a tritone apart. Both the vertical and linear uses of polychords can be seen in the tableau Petrushka’s Room, first in linear motion at rehearsal 49 and then as vertical sonorities at rehearsal 51 in the selected score example. A piano transcription of this tableau shows these harmonies with more visual clarity.
Polychords can be identified with lead-sheet symbols, as shown below.
Polytonality, also called bitonality, occurs when two tonal centers are used at the same time. When this happens in a modal context, the result can be called polymodality or bimodality. Scales or modes that have little in common can be paired, or composers may select scales that have several tones in common. Different registers and timbres may be used to highlight the effect of the two tonalities sounding together. An easy and clear example occurs in Bartok’s Mikrokosmos, No. 105, Game, which features a pentatonic melody in different keys. A gentler example of polytonality can be found in Britten’s The Ash Grove from Folk Songs of the British Isles.
Quartal and Quintal Harmony
Quartal and quintal harmony refers to chords built of fourths and fifths, respectively. These chords came into use after the Common Practice Period as composers sought alternatives to the system of tonal harmony that uses chords built in thirds. Both quartal and quintal chords can have three or more notes, and the usual practice is for the intervals to be perfect, although augmented and diminished fourths are seen in a few quartal harmonies, including in Scriabin’s “mystic” chord. Because P4 intervals invert to P5 intervals, inverted quartal and quintal chords become indistinguishable from one another. The sonority that results includes the stable P5 with an added 2nd or 4th above the bass note, a hallmark sound of 20th century music.
Several examples of quartal harmony appear in Debussy’s Sunken Cathedral, wherein the composer freely uses tertian, quartal, and quintal sonorities. At the opening of the second movement of Bartok’s Piano Concerto No. 2, the strings engage in a beautiful quintal passage that spans 23 measures in length.
Secundal Harmony and Tone Clusters
Secundal harmony uses 2nds and 7ths as harmonic building blocks rather than the thirds found in tertian harmony, and can be constructed in 2nds, 7ths, or in a mixture of the two. Tone clusters (cluster chords) are a type of secundal sonority that are comprised of three or more adjacent notes, and clusters containing two or more m2 intervals are more dissonant than those containing mostly M2 intervals. Tone clusters can be notated traditionally, or may be notated with solid lines and bars, as Henry Cowell did in his piano work The Tides of Manaunaun. Tone clusters on the piano can be played with the fingers, fist, forearm, or a block of wood or other material. Bartok made extensive use of secundal harmony and tone clusters in his Piano Concerto No. 2.
The next example shows a few possibilities for notating secundal harmony and tone clusters.
Parallelism/Planing
Harmonic parallelism or planing is the parallel movement of two or more lines or chords. An example in a tonal environment appears in the third movement of Beethoven’s Piano Sonata Op. 2 No. 1. In the 20th century, planing is often associated with Debussy and Ravel, and its use is a feature of their styles. Both tertian (triads, seventh chords, added note chords) and nontertian sonorities (tone clusters, secundal, quartal, quintal) can be planed. Planing is categorized as diatonic, strict (real), or mixed.
Diatonic planing
In diatonic planing, all voices or chord members follow the pitch classes specified in the scale or mode, as exemplified in Debussy’s Sunken Cathedral. Because only the pitches of the scale are used, vertical sonorities (triad types, etc.) change as different constructions arise within the diatonic scale. Several examples of diatonic planing also occur in Bartok’s Piano Concerto No. 2.
Strict planing
In strict (real) planing, the voices or chord members maintain precise interval relationships, resulting in a sonority that is merely transposed after its first appearance. Debussy’s The Sounds and Fragrances Swirling Through the Evening Air features many instances of planing, including the strict use of parallel major chords.
Mixed planing
In mixed planing, the voices use a blend of diatonic and strict planing, as displayed in Debussy’s Dancers of Delphi.
Rhythm in the 20th Century
Rhythm in the 20th Century - Blackboard pools
- Rhythm in the 20th Century
Overview
Music written during the 20th and 21st centuries has included greater rhythmic freedom and complexity than at any time during the past. Many conventions of western art music during the Common Practice Period such as four measure phrases, the expectation of regular metric downbeats and accents, and the use of standard time signatures and symmetrical meters, have been modified or jettisoned as composers explored new avenues of rhythmic organization. Additionally, the rhythmic practices of nonwestern cultures have continued to make inroads into western art music. The following surveys some of the rhythmic practices that composers of western art music have increasingly used or developed since the late 19th century.
Syncopation
Syncopation happens when a rhythmic pattern obscures the strong beats implied in a time signature, thus creating heightened interest in the music because of the disruption of the normal flow of metric accents. Syncopation has been a feature of many musical styles and genres over the past few centuries and is widely used in 20th and 21st century art music. Syncopation can be used in any meter, at any tempo, and within any level of subdivision of the beat.
A classic and often used example of syncopation is where the usual metric accent pattern is shifted by half a beat. This syncopation can be contained within a bar or can be extended over the bar line by using ties.
Syncopation can also take place within smaller subdivisions of a beat, as shown below.
Hemiola
The hemiola, sometimes called cross-rhythm, is the rhythmic ratio of 3:2. Whether expressed vertically in two parts, or horizontally in one part, the important effect is that of 3 in the space of 2, as illustrated in the next examples.
Displaced Accents (Shifting Accents)
Another method of achieving flexibility in rhythm is through using shifting accents, in which accents are placed on a beat or division of a beat that does not match with the usual metric accent pattern found within that meter. When used consistently, displaced accents can even begin to suggest a different meter. In the following example, a simple duple signature is implied.
Igor Stravinsky used displaced accents in his monumental piece The Rite of Spring. In the episode The Augurs of Spring it is used in a simple duple meter, and in the episode Ritual of Abduction in a compound triple meter. In The Firebird, Stravinsky combines highly syncopated rhythms and displaced accents to radically alter the perception of the meter in the section Infernal Dance of King Kashchei.
Asymmetric/Irregular Meters
A very common way of avoiding the metrical regularity of simple and compound meters is to use asymmetrical meters in which exist groupings of subdivisions of both 2 and 3, making patterns such as 2+3, 3+2, 3+2+2, 2+3+2, and 2+2+3. The two most common asymmetric meters are \(\begin{smallmatrix} 7 \\ 8 \end{smallmatrix}\) and \(\begin{smallmatrix} 5 \\ 8 \end{smallmatrix}\), although others such as \(\begin{smallmatrix} 10 \\ 8 \end{smallmatrix}\) and \(\begin{smallmatrix} 11 \\ 8 \end{smallmatrix}\) are sometimes seen. It is also possible to use the quarter note as the division value, creating meters such as \(\begin{smallmatrix} 5 \\ 4 \end{smallmatrix}\) and \(\begin{smallmatrix} 7 \\ 4 \end{smallmatrix}\). Much less frequently found is the use of the 16th note or smaller values as the division. A piece that features many noteworthy rhythmic devices including meters such as \(\begin{smallmatrix} 18 \\ 16 \end{smallmatrix}\) is Debussy’s Sonata for Flute, Viola, and Harp.
The following example illustrates \(\begin{smallmatrix} 5 \\ 8 \end{smallmatrix}\) and \(\begin{smallmatrix} 7 \\ 8 \end{smallmatrix}\) meters. Note that appropriate beaming makes clear the patterns in these asymmetrical meters.
Complex meters, sometimes called composite meters, are based on more traditional numbers of divisions such as 8 or 9 but that feature beats of unequal length. For instance, the eight 8th notes of \(\begin{smallmatrix} 4 \\ 4 \end{smallmatrix}\) are grouped in four groups of two (2+2+2+2), but in \(\begin{smallmatrix} 8 \\ 8 \end{smallmatrix}\) meter the 8th notes can be expressed in groups of 2+3+3, 3+2+3, and 3+3+2. An example of this occurs in Bartok’s Mikrokosmos, No. 153, Dance in Bulgarian Rhythm. A meter such as \(\begin{smallmatrix} 9 \\ 8 \end{smallmatrix}\) can be transformed into grouping such as 4+2+3. These complex meters are usually notated in the manner shown in the following examples.
Changing Meters/Time Signatures
The use of frequent time signatures changes became common in 20th century music. This practice, also called shifting meter and mixed meter, allows composers to keep the elements of traditional time signatures such as bar lines and metric accents while injecting a fresh and often impelling vibrancy into the music. These shifts in time signature can be very rapid, occurring as often as every measure. For example, the chamber piece Fuging Machine by the author of this text, features a constant shift between \(\begin{smallmatrix} 7 \\ 8 \end{smallmatrix}\)and \(\begin{smallmatrix} 3 \\ 4 \end{smallmatrix}\) throughout most of the work. Another example can be seen in the episode Ritual of Abduction in Stravinsky’s Rite of Spring. While not a requirement, mixed meter often occurs at faster tempos, which helps the listener to perceive the differences in beats, subdivisions of beats, and metric accents. Composers such as Claude Debussy often combined shifting meters, asymmetric meters, and other rhythmic devices in a more gentle and supple manner, as displayed in the previously mentioned Sonata for Flute, Viola, and Harp.
The next example shows a single melodic line that employs shifting meters. As earlier, notice that the beaming makes clear the patterns in the asymmetrical meters (3+2, 2+2+3, etc.).
Ametric/Nonmetric Rhythms
Ametric or nonmetric rhythms occur when a composer writes music that has no audible bar lines or meter. This can include music that uses standard time signatures but in which the music is written in such a way as to obscure the metric accents implied by the time signature, as Edgard Varèse does in his famous piece for solo flute, Density 21.5. An example without time signatures is Charles Ives' Piano Sonata No. 2, Concord, Massachusetts, 1840-1860.
It is also possible to employ all manner of electronic, aleatoric, notational, and improvisational techniques to create music without a perceivable repeating pulse or audible meter.
Added Values
In his book The Technique of My Musical Language, the French composer Olivier Messiaen examines innovative rhythmic ideas and procedures that he used in his own music. These include the techniques of added values, nonretrogradable rhythms, and augmentation and diminution.
In an added value, a short rhythmic value is added to a standard or traditional rhythm. The added value can be accomplished through adding a dot, note, or rest to a rhythmic pattern. The music is ametric and free in feel but is precisely notated.
Messiaen uses added values in “Dance of Fury for Seven Trumpets” from Quartet for the End of Time, a piece written when he was a POW in a German military prison camp. The bar lines do not indicate a specific number of beats or divisions, but instead serve as visual aids to performance, to mark phrase divisions, and to cancel accidentals.
Non-retrogradable Rhythms
A palindrome is a word that is spelled the same backward as forward, such as madam, level, and racecar. A musical palindrome is a rhythm, melody, pitch pattern, or chord progression (for ex., I – ii – V – ii – I) that sounds the same when played forward and backward, and non-retrogradable rhythms are rhythmic palindromes. It is possible to have rather simple non-retrogradable rhythms as well as to combine concepts such as the added value to create more complex examples. Non-retrogradable rhythms can stretch over multiple measures and can conceivably encompass an entire piece. Messiaen is noted for his use of non-retrogradable rhythms.
A simple non-retrogradable rhythm includes this example of syncopation.
Next is a longer and more complex example.
Augmentation and Diminution
Augmentation and diminution are techniques for varying a melody and/or a rhythm and not are new to the 20thcentury, having been used by composers such as J.S. Bach during the Baroque period. Classic or conventional augmentation refers to the doubling of a duration (for ex., quarter notes expanding to half notes) while diminution refers to halving the duration (for ex., quarter notes contracting to eighth notes). Messiaen, in his text The Technique of My Musical Language, includes more complex possibilities by using added values.
Tempo Modulation
In tempo modulation, sometimes called metric modulation, a rhythmic value in the first tempo becomes equal to a new rhythmic value in the second tempo. While it is possible for the time signatures to change, it is not necessary. The following example uses eighth-note triplets to affect the transition, but the device can be extended to other meters and to other tuplets such as quintuplets. Elliott Carter is noted for his use of this technique.
Polyrhythm, Polymeter and Polytempo
The concept of polyrhythm or cross-rhythm has already been touched upon in the section on hemiola. When a hemiola occurs vertically, i.e. in two parts, the effect is that of two distinct rhythmic lines. This practice can be extended to other relationships, such as 5:4 (for ex. a quintuplet vs. eighth notes), 5:2, 7:2 and so forth. To experiment with various ratios, polyrhythm generators can be found online.
Polymeter occurs when two or more meters are used at one time. It is possible to use different time signatures with matching bar lines, or to have two different time signatures with different bar lines. Examples of polymeter in which different time signatures with matching bar lines are used are found in Stravinsky’s ballet score Petrushka at rehearsal 3 (“Introduction”) and rehearsal 14 (“The Crowds”) in the First Tableau: The Shrovetide Fair, and in the Third Tableau: The Moor’s Room at rehearsal 72 (“Waltz”). This piece is also rife with examples of shifting and asymmetric meters. An example of polymeter in which different time signatures are used with different bar lines is the second movement of Maurice Ravel's Piano Trio, in which \(\begin{smallmatrix} 4 \\ 2 \end{smallmatrix}\) is matched with \(\begin{smallmatrix} 3 \\ 4 \end{smallmatrix}\).
Polytempo occurs when two or more tempos are used at a time. A relatively simple example of this is seen in Charles Ives’s chamber early 20th century work The Unanswered Question.
Twelve-Tone Serialism
Twelve-Tone Serialism - Blackboard pools
- Twelve-Tone Serialism
Overview
Composers such as Arnold Schoenberg pushed the chromaticism of late German Romanticism to the breaking point in the closing years of the 19th century with pieces such as Transfigured Night (1899). By the first decade of the 20th century, Schoenberg moved toward atonality, in which dissonances are freed, tertian structures are abandoned, and vertical sonorities consist of any combination of intervals. This style of music fit well with Expressionism, the German visual art and literature style of the early 20th century that reflected sometimes unpleasant inner thoughts rather than pleasant scenes or pictures. Expressionism in Schoenberg’s music is exemplified in pieces such as Three Piano Pieces, Op. 11(1909), Erwartung (1909) and Pierrot Lunaire (1912).
Schoenberg developed the concepts of free or nonserial atonality until the interwar period when his first pieces using the twelve-tone method were written. In twelve-tone serialism, all the pitch classes in the chromatic scale are arranged in a tone-row (tone series) with certain restrictions applied:
- All twelve pitch classes of the chromatic scale must be used in a specific order.
- No pitch class can be repeated until the entire row has sounded, with exceptions made for immediate repetition(s) of a note.
- The series can be inverted (mirror inversion), retrograded (played backward), and transposed.
Tone-rows are typically constructed in a manner that avoids the appearance of a tonal center, tertian structures, and diatonic scales, and should be understood as a logical extension of the atonal music that historically precedes it.
Terminology
Prime – The original or prime (P) form of the row is that which appears at the beginning of a piece.
Retrograde – The retrograde (R) is the original form of the row played backwards.
Inversion – The inversion (I) is the mirror inversion of the original row.
Retrograde Inversion – The retrograde inversion (RI) is the inversion of the original row played backward.
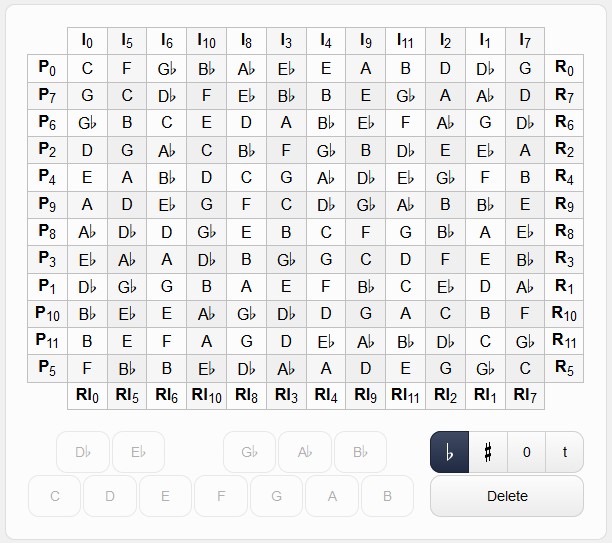
The following examples illustrate these concepts. The prime form (P0) of the row is presented first. Note that the pitch classes can be written with sharps, flats, or a combination of these because of the enharmonic equivalence of notes such as C♯ and D♭. The numbers under the notes are the order numbers and show each note’s position in the row.
Next is the retrograde (R0), which is simply P0 backwards without transposition.
The original row can also be inverted (I0) without transposition. This technique is called mirror inversion and involves analyzing the intervals between the pitch classes in the prime row and then inverting them the same number of semitones in the opposite direction. For example, the first interval in P0 is the P4 (5 semitones) between the C and F. A P4 below C is the note G, but because of octave equivalence this G can be notated a P5 above C or the P4 below.
Retrograde inversion (RI0) is the inversion in reverse order.
Each of these four basic forms can be transposed to begin with any of the twelve pitch classes, which means each row has a total of forty-eight possible permutations. The number that follows the abbreviation (for example, P0) refers to the transposition level of the row. The label P5, for example, indicates that the prime row has been transposed up by 5 semitones and would therefore start on the note F. The label RI7 is simply stating that the retrograde inversion of the row has been transposed up by 7 semitones and would start on the note C.
Twelve-Tone Matrix
The forty-eight possible row forms can be expressed in a 12-tone matrix, which can be generated with online tools, with a phone app, or manually filled in. There are two methods of designating the prime row. The traditional method designates the initial row form encountered in the composition as P0. For example, if a composition begins with the note E, P0 will start with E and P1 will begin a half-step above on an F. The absolute pitch method labels the row that starts on C as P0, which means a row beginning with E would have a transposition level of 4 and be designated P4, even if it were the opening row form encountered in a piece.
It is helpful to understand the process by learning to fill in the matrix manually. The following directions assume the traditional method of row identification and construction. We will use this method in our analysis of 12-tone music.
- Determine the prime row and fill in P0 in the top row of boxes.
- Write the transposition numbers above the matrix. The first pitch is 0, the note a half step above is 1, and so forth. Write these numbers underneath the matrix as well.
- Write the transposition numbers on the left side of the matrix. To find them, subtract each number on top from 12 and write that number in the corresponding space on the left. The first number is always 0.
- Write the notes in the boxes on the left side of the matrix that correspond to the numbers in P0. For example, G is 7 in P0, so it will be written in the box next to the 7 on the left of the matrix.
- Go to the horizontal row that corresponds to the number 1 and transpose P0 up a semitone into that row.
- Continue this process with the horizontal row that corresponds to the number 2, and so forth.
- The diagonal running from the top left to bottom right will always be the first note of P0 in the upper left corner of the matrix.
The following matrix is based upon the prime row discussed thus far. Prime is read left to right, Retrograde right to left, inversion top to bottom, and retrograde inversion bottom to top. This was completed using an online matrix calculator.
Rows can be further subdivided into smaller groupings of ordered notes, including trichords (three notes), tetrachords (four notes), and hexachords (six notes). Each row therefore contains four trichords, three tetrachords, and two hexachords. The interval content in each grouping can be tightly controlled, and some composers have taken advantage of these segments by limiting the intervals found in each grouping to create the same or similar pitch class sets.
In music, row forms can be used in an assortment of ways and are not always clearly shown. They can be overlapped, presented canonically, stacked vertically, and given in different instruments or voices. The first task is to identify the prime row, regardless of whether the traditional or absolute pitch method is used. In Anton Webern’s Wie Bin Ich Froh, P0 occurs in the opening measures of the piano accompaniment but notes 6-9 of the row are stacked in a vertical sonority, making it difficult to determine the correct order. In measure 3, P0 is again stated, and in measure 4 the order number of notes 6-9 becomes clear, allowing the construction of a matrix and the analysis of the row forms used in the piece. The prime row of this piece is F♯ - F♮ - D♮ - E♮ - E♭ - C♮ - A♮ - C♯ - G♯ - B♮ - B♭ - G♮, as illustrated in the next example.
Berg and Webern
Two composers who studied with Schoenberg and who developed the 12-tone method in their own ways are Alban Berg and Anton Webern. Berg and Webern’s early styles were rooted in late German Romanticism, and both followed Schoenberg into atonality and serialism. Of the two, Berg remained the most Romantic and used the twelve-tone technique more freely, as shown in the Violin Concerto, which even quotes a Bach chorale.
Webern’s influence has continued far beyond his unfortunate death during the occupation of Germany following World War II, and he became an admired figure by the post war serial composers. Webern was strict in his use of the twelve-tone method, and his music is highly concentrated, with some movements less than a minute long. His music is noted for its use of soft dynamics, pointillistic and transparent textures, brilliant orchestration, the use of special effects (mutes, harmonics, flutter tonguing), a reliance on canonic writing such as the double canons in the Symphony Op. 21 (1928), and tightly organized and highly atonal tone rows.
Integral Serialism
Integral or total serialism is an extension of twelve-tone technique, particularly that of Webern, who was a primary model for the post WWII serial composers such as Karlheinz Stockhausen and Pierre Boulez. Integral serialism can include the serialization of rhythm, dynamics, register, articulation, row form, and timbre, and shows the search for the total control over all aspects of music. Another significant figure in this technique was Milton Babbitt, who originated the concept of using a matrix (or “square”) to list the 48 permutations for a given 12-tone row.
Other 20th Century Techniques
Other 20th and 21st Century Techniques - Blackboard pools
- Other 20th and 21st Century Techniques
Overview
Entire volumes can be written about many of the topics covered in this text, and this is equally true when examining the new paths that composers have forged since the end of the 19th century. The increasing influence of global resources on western art music have been profound, the advance in electronics and computer-generated music has been astounding, and new popular styles and genres have germinated and grown to maturity over in a strikingly brief period of time. It is therefore impossible to do more than provide a short overview of composers, influences, styles, and techniques, which will hopefully provide some sort of framework for the understanding of the rich diversity of practice and thought that has grown during this period.
We will confine our brief overview to the following areas, which have proven to be some of the more fertile ground in which music has grown:
- Indeterminacy
- Graphic Notation
- Minimalism
Indeterminacy / Aleatory / Chance Music
Indeterminacy and aleatory both refer to the inclusion of chance in music. In the mid-20th century, composers began to assign major creative roles to the performer and to random chance in the compositional process, in part as a reaction to the total organization of integral serialism. Composers can introduce aleatoric elements into a piece by leaving some or all musical parameters to random generation. Randomization of musical parameters can be accomplished by rolling dice, using an app, or in other ways determined by the composer. Composers also inject chance into music by allowing the performer(s) to determine some or all musical parameters. When doing so, composers often abandon traditional musical notation and instead utilize some sort of graphic notation to convey the ideas, which allows great freedom to be achieved. When chance is left to the performer(s), different performances of the same work may vary greatly, and the receptiveness, musical sensitivity, and improvisational imagination of the performer(s) becomes of far greater consequence than in traditionally notated music.
John Cage
John Cage is one of the most influential music thinkers in the last of 20th century. Cage studied with Cowell and Schoenberg and was influenced by Varese and Zen Buddhism. He was a prolific writer and champion of Avant Garde music who believed that music could include all types of noise. He thought that standard methods of composition were limiting because they did not use what he termed the “entire field of sound,” and gradually evolved the idea that music was a “purposeless play.” His development and use of indeterminacy continue to resonate into the 21st century. While indeterminacy was used by earlier 20th century composers including Charles Ives and Henry Cowell, Cage’s efforts helped to legitimize indeterminate procedures in music and lead to its broader acceptance in the 1950s.
During the period of the 1930s-50s, Cage wrote experimental music using unconventional instruments such as brake drums, flowerpots, electrical buzzers, microphones, and generator noise. It was during this time in the 1940s that he composed the Sonatas and Interludes for solo piano (1948) for “prepared piano,” which is simply a piano with screws, pieces of wood, and rubber wedges inserted on and between the strings.
His best-known work is 4’33’’, in which he brought the ideals of indeterminacy to their ultimate conclusion. The score consists of three roman numerals followed by the word “tacit.” The performer(s) are to remain silent during the entire work. The piece features an absence of musical materials and musical sounds, allowing silence to be as important as traditionally notated music. The focus is on the happenings in the concert hall such as audience and environmental noises. Cage considered this piece to be his most significant work.
Graphic Notation
Graphic notation (a.k.a. graphic score) began in the mid-20th century when composers interested in the infusion of aleatoric elements in music began to use a variety of visual symbols in place of traditional music notation. The imagination of the composer is the only limit as to what can be used, and the interpretation and realization of these scores can vary widely. Good introductions can be found on YouTube, and the ensuing list features a variety of websites and YouTube videos.
Further resources include:
- An article in The Guardian from 2013 about visual scores that “rival the best contemporary art.”
- An article from the Lawrence Public Library
- The Classic FM article about Theresa Sauer’s book Notations21.
- An Artbouillon article on John Cage from 2012 that features photos of several Cage scores.
- YouTube – Recording and score of John Cage’s Imaginary Landscape No. 5 - 1952.
- YouTube – Recording and score of Iannis Xenakis’ Metastasis.
- YouTube – Recording and score of Krzysztof Penderecki’s Threnody for the Victims of Hiroshima, which is an example of proportional notation in which durations are suggested through timings.
- YouTube – Recording and score of George Crumb’s Makrokosmos I.
- YouTube – Recording and score of Karlheinz Stockhausen’s electronic piece Studie II.
Minimalism
Minimalism’s origins are in the music of Cage, Eastern music and philosophy, and the visual arts of the 1950s. Minimalist composers desired to reduce music to a much simpler style, in contrast to the highly organized and complex sounding music of twelve-tone serialism. Early minimalist music shows a great economy in musical resources, but the term minimalism imperfectly fits the music of the 1970s and later because of its increasing complexity and inclusion of varied musical resources, including more traditional harmonic progression.
Features of minimalist music include use of the following:
- Limited pitches
- Consonant sonorities
- Additive process
- Simple rhythms and steady pulse
- Diatonic tonal and modal resources and scales
- Repetition
- Phase shifting
- Drones and ostinatos
The most significant composers who were at the forefront of developing this style were La Monte Young, Terry Riley, Steve Reich, and Philip Glass.
La Monte Young
La Monte Young was influenced by Indian music, studying with the Indian singer Pandit Pran Nath. He is interested in non-equal temperament tunings like just intonation. His early work Composition 1960 No. 7 consists of a single event – a P5 (B-F♯) that is “to be held for a very long time,” as he writes in the score.
Terry Riley
Terry Riley, like Young, studied Indian music with Pran Nath. Riley adopted the use of repetitive interlocking melodic patterns in his music, was interested in electronic music, and experimented with tape loops in the early 1960s. His influential work In C (1964) consists of melodic patterns quoted from 18thcentury music and is scored for any number of any kind of instruments and performers. Instrumentalists are directed to play through the 53 fragments at any tempo and repeating individual fragments as often as desired before moving to next fragment. During this, steady 8th note C’s are played in upper register of the piano.
Steve Reich
Steve Reich studied African and Balinese music. He discovered phase shifting – in which two identical recordings gradually go out of synchronization – while working with tape loops in the mid-1960s. Two pieces from this period are It’s Gonna Rain (1965) and Come Out (1966). He began applying phase shifting to live performance with his 1967 piece for two pianos, Piano Phase (1967). Reich’s style consists of diatonic melodic figures, steady rhythmic pulsation, and percussive attacks. Other significant pieces include Music for Eighteen Musicians (1976), Vermont Counterpoint (1982), and The Desert Music (1982).
Philip Glass
Philip Glass became interested in the additive rhythm approach from his studies of Indian Music. For example, Music in Fifths (1969) contains an eight-note figure that is expanded through this additive process to include 200 notes. Glass’s music gradually moved away from earlier efforts to a style that contains more complexity and harmonic progression. In Another Look at Harmony (1975) he began to use tonal harmonic progressions. His operas Einstein on the Beach (1975) and Akhnaten (1983) have gained wide acclaim.
John Adams
John Adams is a Harvard educated clarinetist, conductor and composer who writes in a post-minimalist and neoromantic style. He has written in a variety of genres but is best known for his operas and orchestral music. An early and important work for string orchestra, Shaker Loops (1978) shows his strong minimalist influences. Grand Pianola Music (1982), for small orchestra, percussion and three sopranos, showcases the V – I progression in its finale “On the Dominant Divide.” Harmonielehre (1985) remains one of his best-known works, with grand, romantic qualities and a bold, brassy, heroic ending. The 1996 piano concerto Century Rolls is inspired by player piano music.
Adams’ operas are usually based on real people and real events. Nixon in China (1987) is about
Nixon’s 1970s visit to China, The Death of Klinghofer (1989) is about the Palestinian hijacking of
the cruise liner Achille Lauro, and Doctor Atomic (2005) focuses on the events surrounding the creation of the first atomic bomb.
Michael Torke
Michael Torke is a post-minimalist composer whose music features colorful and brilliant orchestration, an essentially tonal outlook, driving rhythms, and influences that range from jazz and pop to Debussy and Stravinsky. Representative works include Bright Blue Music (1985), Javelin (for the 1996 Olympics), Adjustable Wrench (1987), Blue Pacific (2006), and Unconquered (2016).